Plot a 2 Way ANOVA using dplyr and ggplot2

Source: R/Plot2WayANOVA.R

Takes a formula and a dataframe as input, conducts an analysis of variance prints the results (AOV summary table, table of overall model information and table of means) then uses ggplot2 to plot an interaction graph (line or bar) . Also uses Brown-Forsythe test for homogeneity of variance. Users can also choose to save the plot out as a png file.

Plot2WayANOVA(formula,
               dataframe = NULL,
               confidence=.95,
               plottype = "line",
               errorbar.display = "CI",
               xlab = NULL,
               ylab = NULL,
               title = NULL,
               subtitle = NULL,
               interact.line.size = 2,
               ci.line.size = 1,
               mean.label = FALSE,
               mean.ci = TRUE,
               mean.size = 4,
               mean.shape = 23,
               mean.color = "darkred",
               mean.label.size = 3,
               mean.label.color = "black",
               offset.style = "none",
               overlay.type = NULL,
               posthoc.method = "scheffe",
               show.dots = FALSE,
               PlotSave = FALSE,
               ggtheme = ggplot2::theme_bw(),
               package = "RColorBrewer",
               palette = "Dark2",
               ggplot.component = NULL)

Arguments

formula

a formula with a numeric dependent (outcome) variable, and two independent (predictor) variables e.g. mpg ~ am * vs. The independent variables are coerced to factors (with warning) if possible.
dataframe

a dataframe or an object that can be coerced to a dataframe
confidence

what confidence level for confidence intervals
plottype

bar or line (quoted)
errorbar.display

default "CI" (confidence interval), which type of errorbar should be displayed around the mean point? Other options include "SEM" (standard error of the mean) and "SD" (standard dev). "none" removes it entirely much like interaction.plot
xlab, ylab

Labels for `x` and `y` axis variables. If `NULL` (default), variable names for `x` and `y` will be used.
title

The text for the plot title. A generic default is provided.
subtitle

The text for the plot subtitle. If `NULL` (default), key model information is provided as a subtitle.
interact.line.size

Line size for the line connecting the group means (Default: `2`).
ci.line.size

Line size for the confidence interval bracketing the group means (Default: `1`).
mean.label

Logical that decides whether the value of the group mean is to be displayed (Default: `FALSE`).
mean.ci

Logical that decides whether the confidence interval for group means is to be displayed (Default: `TRUE`).
mean.size

Point size for the data point corresponding to mean (Default: `4`).
mean.shape

Shape of the plot symbol for the mean (Default: `23` which is a diamond).
mean.color

Color for the data point corresponding to mean (Default: `"darkred"`).
mean.label.size, mean.label.color

Aesthetics for the label displaying mean. Defaults: `3`, `"black"`, respectively.
offset.style

A character string (e.g., `"wide"` or `"narrow"`, or `"none"`) which controls whether items are offset from the centerline for clarity. Useful when you want to add individual datapoints or confdence interval lines overlap. (Default: `"none"`).
overlay.type

A character string (e.g., `"box"` or `"violin"`), if you wish to overlay that information on factor1
posthoc.method

A character string, one of "hsd", "bonf", "lsd", "scheffe", "newmankeuls", defining the method for the pairwise comparisons. (Default: `"scheffe"`).
show.dots

Logical that decides whether the individual data points are displayed (Default: `FALSE`).
PlotSave

a logical indicating whether the user wants to save the plot as a png file
ggtheme

A function, ggplot2 theme name. Default value is ggplot2::theme_bw(). Any of the ggplot2 themes, or themes from extension packages are allowed (e.g., hrbrthemes::theme_ipsum(), etc.).
package

Name of package from which the palette is desired as string or symbol.
palette

Name of palette as string or symbol.
ggplot.component

A ggplot component to be added to the plot prepared. The default is NULL. The argument should be entered as a function. for example to change the size and color of the x axis text you use: `ggplot.component = theme(axis.text.x = element_text(size=13, color="darkred"))` depending on what theme is in use the ggplot component might not work as expected.

Value

A list with 5 elements which is returned invisibly. These items are always sent to the console for display but for user convenience the function also returns a named list with the following items in case the user desires to save them or further process them - $ANOVATable, $ModelSummary, $MeansTable, $PosthocTable, $BFTest, and $SWTest. The plot is always sent to the default plot device

Details

Details about how the function works in order of steps taken.

  1. Some basic error checking to ensure a valid formula and dataframe. Only accepts fully *crossed* formula to check for interaction term

  2. Ensure the dependent (outcome) variable is numeric and that the two independent (predictor) variables are or can be coerced to factors -- user warned on the console

  3. Remove missing cases -- user warned on the console

  4. Calculate a summarized table of means, sds, standard errors of the means, confidence intervals, and group sizes.

  5. Use aov function to execute an Analysis of Variance (ANOVA)

  6. Use sjstats::anova_stats to calculate eta squared and omega squared values per factor. If the design is unbalanced warn the user and use Type II sums of squares

  7. Produce a standard ANOVA table with additional columns

  8. Use the PostHocTest for producing a table of post hoc comparisons for all effects that were significant

  9. Testing Homogeneity of Variance assumption with Brown-Forsythe test

  10. Use the PostHocTest for conducting post hoc tests for effects that were significant

  11. Use the shapiro.test for testing normality assumption with Shapiro-Wilk

  12. Use ggplot2 to plot an interaction plot of the type the user specified.

The defaults are deliberately constructed to emphasize the nature of the interaction rather than focusing on distributions. So while a violin plot of the first factor by level is displayed along with dots for individual data points shaded by the second factor, the emphasis is on the interaction lines.

References

: ANOVA: Delacre, Leys, Mora, & Lakens, *PsyArXiv*, 2018

See also

aov, BrownForsytheTest, sjstats::anova_stats, replications, shapiro.test, interaction.plot

Author

Chuck Powell

Examples


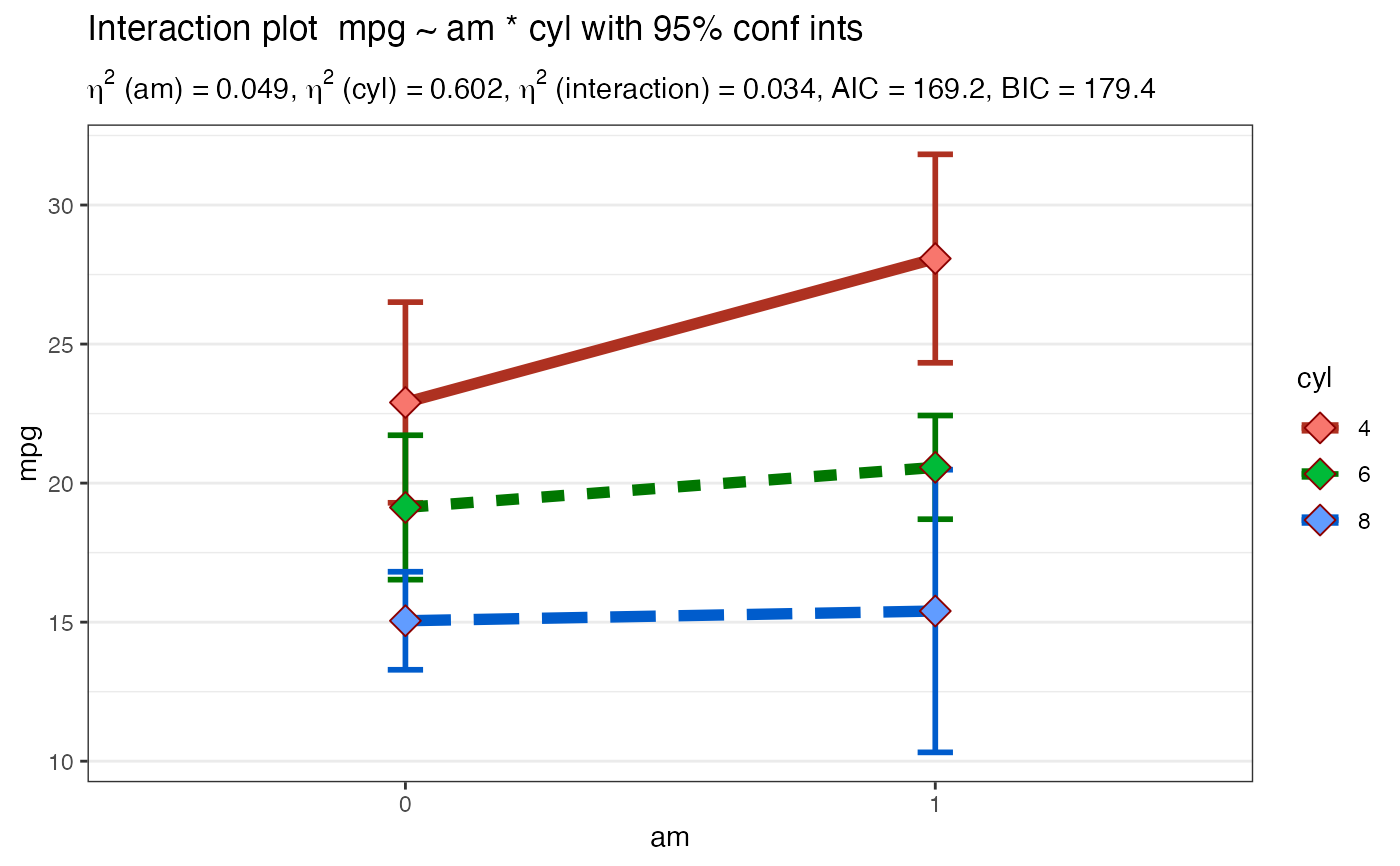
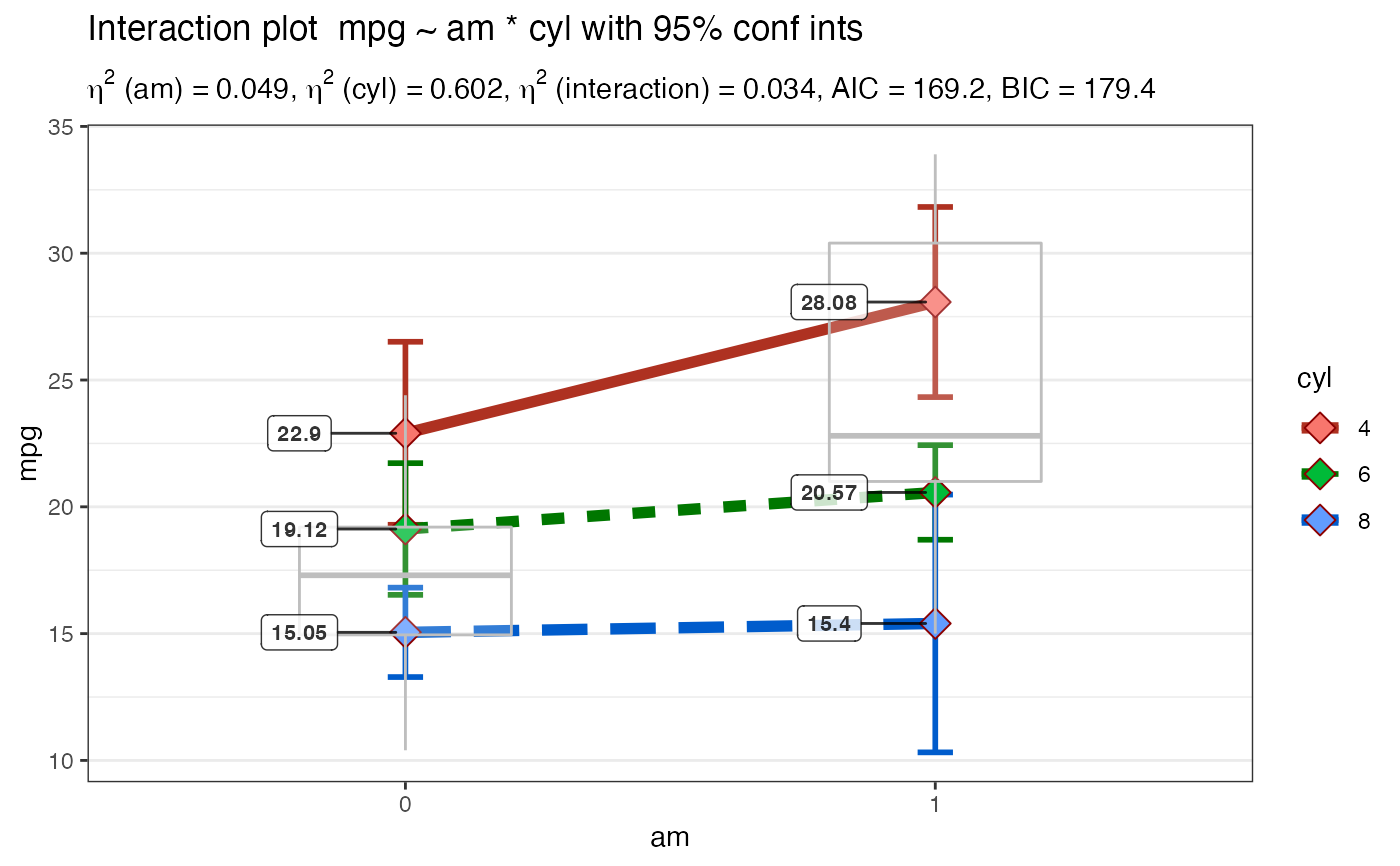
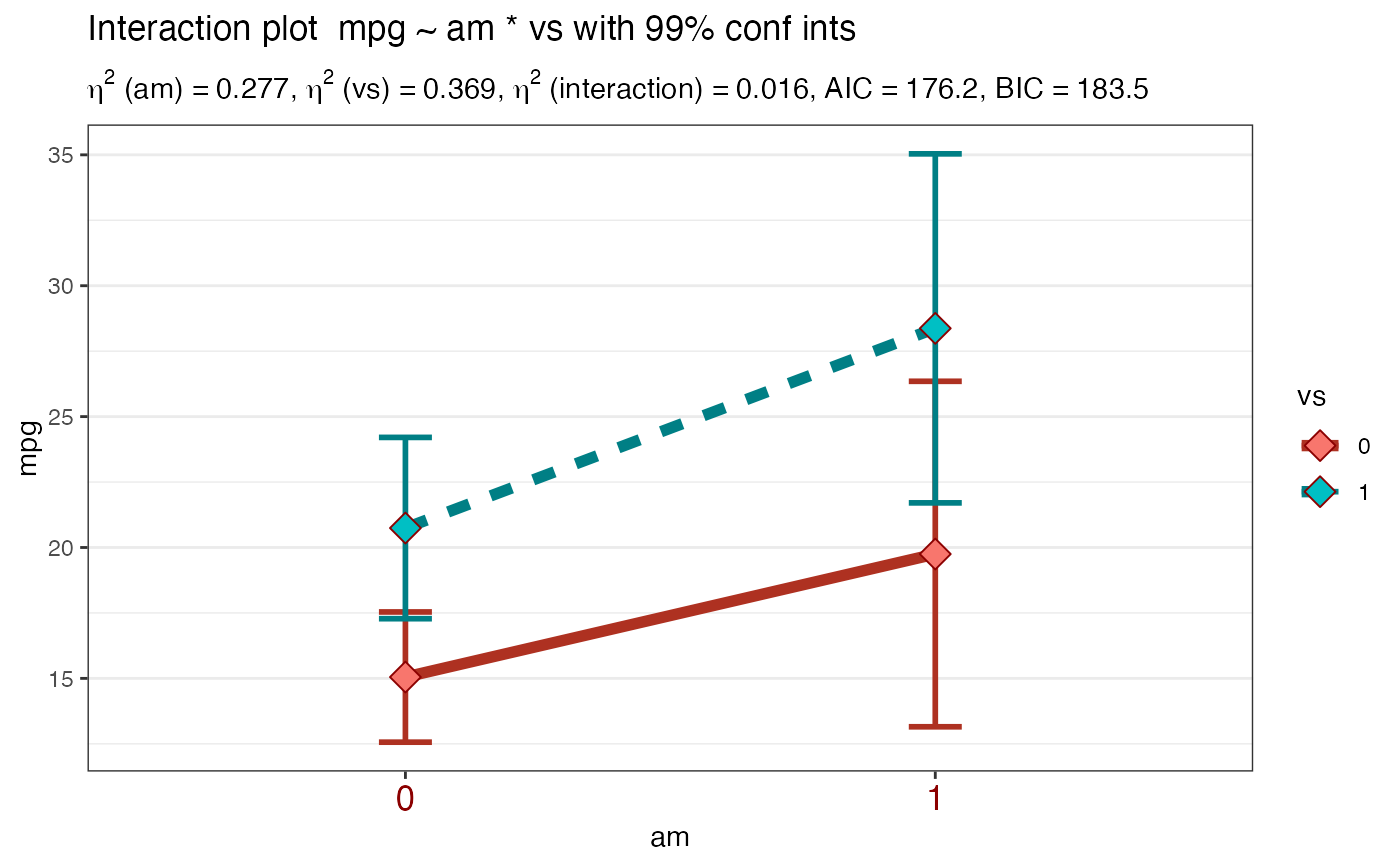
Plot2WayANOVA(mpg ~ am * cyl, mtcars, plottype = "line")

#> 
#> Converting am to a factor --- check your results
#> 
#> Converting cyl to a factor --- check your results
#> 
#> 				--- WARNING! ---
#> 		You have one or more cells with less than 3 observations.
#> # A tibble: 6 x 3
#>   am    cyl   count
#>   <fct> <fct> <dbl>
#> 1 0     4         3
#> 2 0     6         4
#> 3 0     8        12
#> 4 1     4         8
#> 5 1     6         3
#> 6 1     8         2
#> 
#> 				--- WARNING! ---
#> 		You have an unbalanced design. Using Type II sum of 
#>             squares, to calculate factor effect sizes eta and omega.
#>             Your two factors account for 0.684 of the type II sum of 
#>             squares.
#>             term   sumsq  meansq df statistic p.value etasq partial.etasq
#> am            am  36.767  36.767  1     3.999   0.056 0.049         0.133
#> cyl          cyl 456.401 228.200  2    24.819   0.000 0.602         0.656
#> am:cyl    am:cyl  25.437  12.718  2     1.383   0.269 0.034         0.096
#> ...4   Residuals 239.059   9.195 26        NA      NA    NA            NA
#>        omegasq partial.omegasq epsilonsq cohens.f power
#> am       0.036           0.086     0.036    0.392 0.515
#> cyl      0.571           0.598     0.578    1.382 1.000
#> am:cyl   0.009           0.023     0.009    0.326 0.298
#> ...4        NA              NA        NA       NA    NA
#> 
#> Table of group means
#> # A tibble: 6 x 15
#> # Groups:   am [2]
#>   am    cyl   TheMean TheSD TheSEM CIMuliplier LowerBoundCI UpperBoundCI
#>   <fct> <fct>   <dbl> <dbl>  <dbl>       <dbl>        <dbl>        <dbl>
#> 1 0     4        22.9 1.45   0.839        4.30         19.3         26.5
#> 2 0     6        19.1 1.63   0.816        3.18         16.5         21.7
#> 3 0     8        15.0 2.77   0.801        2.20         13.3         16.8
#> 4 1     4        28.1 4.48   1.59         2.36         24.3         31.8
#> 5 1     6        20.6 0.751  0.433        4.30         18.7         22.4
#> 6 1     8        15.4 0.566  0.4         12.7          10.3         20.5
#> # … with 7 more variables: LowerBoundSEM <dbl>, UpperBoundSEM <dbl>,
#> #   LowerBoundSD <dbl>, UpperBoundSD <dbl>, N <int>, LowerBound <dbl>,
#> #   UpperBound <dbl>
#> 
#> Post hoc tests for all effects that were significant
#> 
#>   Posthoc multiple comparisons of means: Scheffe Test 
#>     95% family-wise confidence level
#> 
#> $cyl
#>          diff     lwr.ci     upr.ci    pval    
#> 6-4 -4.756706 -10.029278  0.5158655 0.09684 .  
#> 8-4 -7.329581 -11.723391 -2.9357710 0.00024 ***
#> 8-6 -2.572874  -7.620978  2.4752288 0.64828    
#> 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> 
#> Testing Homogeneity of Variance with Brown-Forsythe 
#>    *** Possible violation of the assumption ***
#> Brown-Forsythe Test for Homogeneity of Variance using median
#>       Df F value  Pr(>F)  
#> group  5   2.736 0.04086 *
#>       26                  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Testing Normality Assumption with Shapiro-Wilk 
#> 
#> 	Shapiro-Wilk normality test
#> 
#> data:  MyAOV_residuals
#> W = 0.96277, p-value = 0.3263
#> 
#> 
#> Bayesian analysis of models in order
#> # A tibble: 4 x 4
#>   model                    bf support                        margin_of_error
#>   <chr>                 <dbl> <chr>                                    <dbl>
#> 1 am + cyl          4228908.  " data support is extreme"        0.0124      
#> 2 am + cyl + am:cyl 3083523.  " data support is extreme"        0.0224      
#> 3 cyl               2274206.  " data support is extreme"        0.0000000127
#> 4 am                     86.6 " data support is very strong"    0.000000217 
#> 
#> Interaction graph plotted...
Plot2WayANOVA(mpg ~ am * cyl,
  mtcars,
  plottype = "line",
  overlay.type = "box",
  mean.label = TRUE
)

#> 
#> Converting am to a factor --- check your results
#> 
#> Converting cyl to a factor --- check your results
#> 
#> 				--- WARNING! ---
#> 		You have one or more cells with less than 3 observations.
#> # A tibble: 6 x 3
#>   am    cyl   count
#>   <fct> <fct> <dbl>
#> 1 0     4         3
#> 2 0     6         4
#> 3 0     8        12
#> 4 1     4         8
#> 5 1     6         3
#> 6 1     8         2
#> 
#> 				--- WARNING! ---
#> 		You have an unbalanced design. Using Type II sum of 
#>             squares, to calculate factor effect sizes eta and omega.
#>             Your two factors account for 0.684 of the type II sum of 
#>             squares.
#>             term   sumsq  meansq df statistic p.value etasq partial.etasq
#> am            am  36.767  36.767  1     3.999   0.056 0.049         0.133
#> cyl          cyl 456.401 228.200  2    24.819   0.000 0.602         0.656
#> am:cyl    am:cyl  25.437  12.718  2     1.383   0.269 0.034         0.096
#> ...4   Residuals 239.059   9.195 26        NA      NA    NA            NA
#>        omegasq partial.omegasq epsilonsq cohens.f power
#> am       0.036           0.086     0.036    0.392 0.515
#> cyl      0.571           0.598     0.578    1.382 1.000
#> am:cyl   0.009           0.023     0.009    0.326 0.298
#> ...4        NA              NA        NA       NA    NA
#> 
#> Table of group means
#> # A tibble: 6 x 15
#> # Groups:   am [2]
#>   am    cyl   TheMean TheSD TheSEM CIMuliplier LowerBoundCI UpperBoundCI
#>   <fct> <fct>   <dbl> <dbl>  <dbl>       <dbl>        <dbl>        <dbl>
#> 1 0     4        22.9 1.45   0.839        4.30         19.3         26.5
#> 2 0     6        19.1 1.63   0.816        3.18         16.5         21.7
#> 3 0     8        15.0 2.77   0.801        2.20         13.3         16.8
#> 4 1     4        28.1 4.48   1.59         2.36         24.3         31.8
#> 5 1     6        20.6 0.751  0.433        4.30         18.7         22.4
#> 6 1     8        15.4 0.566  0.4         12.7          10.3         20.5
#> # … with 7 more variables: LowerBoundSEM <dbl>, UpperBoundSEM <dbl>,
#> #   LowerBoundSD <dbl>, UpperBoundSD <dbl>, N <int>, LowerBound <dbl>,
#> #   UpperBound <dbl>
#> 
#> Post hoc tests for all effects that were significant
#> 
#>   Posthoc multiple comparisons of means: Scheffe Test 
#>     95% family-wise confidence level
#> 
#> $cyl
#>          diff     lwr.ci     upr.ci    pval    
#> 6-4 -4.756706 -10.029278  0.5158655 0.09684 .  
#> 8-4 -7.329581 -11.723391 -2.9357710 0.00024 ***
#> 8-6 -2.572874  -7.620978  2.4752288 0.64828    
#> 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> 
#> Testing Homogeneity of Variance with Brown-Forsythe 
#>    *** Possible violation of the assumption ***
#> Brown-Forsythe Test for Homogeneity of Variance using median
#>       Df F value  Pr(>F)  
#> group  5   2.736 0.04086 *
#>       26                  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Testing Normality Assumption with Shapiro-Wilk 
#> 
#> 	Shapiro-Wilk normality test
#> 
#> data:  MyAOV_residuals
#> W = 0.96277, p-value = 0.3263
#> 
#> 
#> Bayesian analysis of models in order
#> # A tibble: 4 x 4
#>   model                    bf support                        margin_of_error
#>   <chr>                 <dbl> <chr>                                    <dbl>
#> 1 am + cyl          4187558.  " data support is extreme"        0.0106      
#> 2 am + cyl + am:cyl 3113288.  " data support is extreme"        0.0263      
#> 3 cyl               2274206.  " data support is extreme"        0.0000000127
#> 4 am                     86.6 " data support is very strong"    0.000000217 
#> 
#> Interaction graph plotted...

library(ggplot2)
Plot2WayANOVA(mpg ~ am * vs, 
  mtcars, 
  confidence = .99,
  ggplot.component = theme(axis.text.x = element_text(size=13, color="darkred")))

#> 
#> Converting am to a factor --- check your results
#> 
#> Converting vs to a factor --- check your results
#> 
#> 				--- WARNING! ---
#> 		You have an unbalanced design. Using Type II sum of 
#>             squares, to calculate factor effect sizes eta and omega.
#>             Your two factors account for 0.661 of the type II sum of 
#>             squares.
#>            term   sumsq  meansq df statistic p.value etasq partial.etasq
#> am           am 276.033 276.033  1    22.902   0.000 0.277         0.450
#> vs           vs 367.411 367.411  1    30.484   0.000 0.369         0.521
#> am:vs     am:vs  16.010  16.010  1     1.328   0.259 0.016         0.045
#> ...4  Residuals 337.476  12.053 28        NA      NA    NA            NA
#>       omegasq partial.omegasq epsilonsq cohens.f power
#> am      0.262           0.406     0.265    0.904 0.998
#> vs      0.352           0.480     0.356    1.043 1.000
#> am:vs   0.004           0.010     0.004    0.218 0.211
#> ...4       NA              NA        NA       NA    NA
#> 
#> Table of group means
#> # A tibble: 4 x 15
#> # Groups:   am [2]
#>   am    vs    TheMean TheSD TheSEM CIMuliplier LowerBoundCI UpperBoundCI
#>   <fct> <fct>   <dbl> <dbl>  <dbl>       <dbl>        <dbl>        <dbl>
#> 1 0     0        15.0  2.77  0.801        3.11         12.6         17.5
#> 2 0     1        20.7  2.47  0.934        3.71         17.3         24.2
#> 3 1     0        19.8  4.01  1.64         4.03         13.2         26.3
#> 4 1     1        28.4  4.76  1.80         3.71         21.7         35.0
#> # … with 7 more variables: LowerBoundSEM <dbl>, UpperBoundSEM <dbl>,
#> #   LowerBoundSD <dbl>, UpperBoundSD <dbl>, N <int>, LowerBound <dbl>,
#> #   UpperBound <dbl>
#> 
#> Post hoc tests for all effects that were significant
#> 
#>   Posthoc multiple comparisons of means: Scheffe Test 
#>     99% family-wise confidence level
#> 
#> $am
#>         diff   lwr.ci   upr.ci    pval    
#> 1-0 7.244939 2.619029 11.87085 5.3e-05 ***
#> 
#> $vs
#>         diff   lwr.ci   upr.ci    pval    
#> 1-0 6.732986 2.153198 11.31277 0.00013 ***
#> 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> 
#> Testing Homogeneity of Variance with Brown-Forsythe 
#> Brown-Forsythe Test for Homogeneity of Variance using median
#>       Df F value Pr(>F)
#> group  3  0.8809 0.4629
#>       28               
#> 
#> Testing Normality Assumption with Shapiro-Wilk 
#> 
#> 	Shapiro-Wilk normality test
#> 
#> data:  MyAOV_residuals
#> W = 0.97845, p-value = 0.7535
#> 
#> 
#> Bayesian analysis of models in order
#> # A tibble: 4 x 4
#>   model                 bf support                        margin_of_error
#>   <chr>              <dbl> <chr>                                    <dbl>
#> 1 am + vs         200567.  " data support is extreme"       0.0153       
#> 2 am + vs + am:vs 123044.  " data support is extreme"       0.0140       
#> 3 vs                 529.  " data support is extreme"       0.00000000901
#> 4 am                  86.6 " data support is very strong"   0.000000217  
#> 
#> Interaction graph plotted...