CHAID and caret – a good combo – June 6, 2018
Tagged as: [In an earlier post I focused on
an in depth visit with CHAID (Chi-square automatic interaction
detection). There are lots of tools that can help you predict an
outcome, or classify, but CHAID is especially good at helping you
explain to any audience how the model arrives at it’s prediction or
classification. It’s also incredibly robust from a statistical
perspective, making almost no assumptions about your data for
distribution or normality. This post I’ll focus on marrying CHAID with
the awesome caret package
to make our predicting easier and hopefully more accurate. Although not
strictly necessary you’re probably best served by reading the original
post first.
We’ve been using a dataset that comes to us from the IBM Watson
Project
and comes packaged with the rsample library. It’s a very practical and
understandable dataset. A great use case for a tree based algorithm.
Imagine yourself in a fictional company faced with the task of trying to
figure out which employees you are going to “lose” a.k.a. attrition or
turnover. There’s a steep cost involved in keeping good employees, and
training and on-boarding can be expensive. Being able to predict
attrition even a little bit better would save you lots of money and make
the company better, especially if you can understand exactly what you
have to “watch out for” that might indicate the person is a high risk to
leave.
Setup and library loading
If you’ve never used CHAID before you may also not have partykit.
CHAID isn’t on CRAN but I have commented out the install command
below. You’ll also get a variety of messages, none of which is relevant
to this example so I’ve suppressed them.
# install.packages("partykit")
# install.packages("CHAID", repos="http://R-Forge.R-project.org")
require(rsample) # for dataset and splitting also loads broom and tidyr
require(dplyr)
require(CHAID)
require(purrr) # we'll use it to consolidate some data
require(caret)
require(kableExtra) # just to make the output nicer
Predicting attrition in a fictional company
Last time I spent a great deal
of time explaining the mechanics of loading the data. This time we’ll
race right through. If you need an explanation of what’s going on please
refer back. I’ve embedded some comments in the code to follow along and
changing the data frame name to newattrit is not strictly necessary it
just mimics the last post.
str(attrition) # included in rsample
## 'data.frame': 1470 obs. of 31 variables:
## $ Age : int 41 49 37 33 27 32 59 30 38 36 ...
## $ Attrition : Factor w/ 2 levels "No","Yes": 2 1 2 1 1 1 1 1 1 1 ...
## $ BusinessTravel : Factor w/ 3 levels "Non-Travel","Travel_Frequently",..: 3 2 3 2 3 2 3 3 2 3 ...
## $ DailyRate : int 1102 279 1373 1392 591 1005 1324 1358 216 1299 ...
## $ Department : Factor w/ 3 levels "Human_Resources",..: 3 2 2 2 2 2 2 2 2 2 ...
## $ DistanceFromHome : int 1 8 2 3 2 2 3 24 23 27 ...
## $ Education : Ord.factor w/ 5 levels "Below_College"<..: 2 1 2 4 1 2 3 1 3 3 ...
## $ EducationField : Factor w/ 6 levels "Human_Resources",..: 2 2 5 2 4 2 4 2 2 4 ...
## $ EnvironmentSatisfaction : Ord.factor w/ 4 levels "Low"<"Medium"<..: 2 3 4 4 1 4 3 4 4 3 ...
## $ Gender : Factor w/ 2 levels "Female","Male": 1 2 2 1 2 2 1 2 2 2 ...
## $ HourlyRate : int 94 61 92 56 40 79 81 67 44 94 ...
## $ JobInvolvement : Ord.factor w/ 4 levels "Low"<"Medium"<..: 3 2 2 3 3 3 4 3 2 3 ...
## $ JobLevel : int 2 2 1 1 1 1 1 1 3 2 ...
## $ JobRole : Factor w/ 9 levels "Healthcare_Representative",..: 8 7 3 7 3 3 3 3 5 1 ...
## $ JobSatisfaction : Ord.factor w/ 4 levels "Low"<"Medium"<..: 4 2 3 3 2 4 1 3 3 3 ...
## $ MaritalStatus : Factor w/ 3 levels "Divorced","Married",..: 3 2 3 2 2 3 2 1 3 2 ...
## $ MonthlyIncome : int 5993 5130 2090 2909 3468 3068 2670 2693 9526 5237 ...
## $ MonthlyRate : int 19479 24907 2396 23159 16632 11864 9964 13335 8787 16577 ...
## $ NumCompaniesWorked : int 8 1 6 1 9 0 4 1 0 6 ...
## $ OverTime : Factor w/ 2 levels "No","Yes": 2 1 2 2 1 1 2 1 1 1 ...
## $ PercentSalaryHike : int 11 23 15 11 12 13 20 22 21 13 ...
## $ PerformanceRating : Ord.factor w/ 4 levels "Low"<"Good"<"Excellent"<..: 3 4 3 3 3 3 4 4 4 3 ...
## $ RelationshipSatisfaction: Ord.factor w/ 4 levels "Low"<"Medium"<..: 1 4 2 3 4 3 1 2 2 2 ...
## $ StockOptionLevel : int 0 1 0 0 1 0 3 1 0 2 ...
## $ TotalWorkingYears : int 8 10 7 8 6 8 12 1 10 17 ...
## $ TrainingTimesLastYear : int 0 3 3 3 3 2 3 2 2 3 ...
## $ WorkLifeBalance : Ord.factor w/ 4 levels "Bad"<"Good"<"Better"<..: 1 3 3 3 3 2 2 3 3 2 ...
## $ YearsAtCompany : int 6 10 0 8 2 7 1 1 9 7 ...
## $ YearsInCurrentRole : int 4 7 0 7 2 7 0 0 7 7 ...
## $ YearsSinceLastPromotion : int 0 1 0 3 2 3 0 0 1 7 ...
## $ YearsWithCurrManager : int 5 7 0 0 2 6 0 0 8 7 ...
# the easy to convert because they are integers with less than 10 levels
attrition <- attrition %>%
mutate_if(function(col) length(unique(col)) <= 10 & is.integer(col), as.factor)
# More difficult to get 5 levels
attrition$YearsSinceLastPromotion <- cut(
attrition$YearsSinceLastPromotion,
breaks = c(-1, 0.9, 1.9, 2.9, 30),
labels = c("Less than 1", "1", "2", "More than 2")
)
# everything else just five more or less even levels
attrition <- attrition %>%
mutate_if(is.numeric, funs(cut_number(., n=5)))
dim(attrition)
## [1] 1470 31
str(attrition)
## 'data.frame': 1470 obs. of 31 variables:
## $ Age : Factor w/ 5 levels "[18,29]","(29,34]",..: 4 5 3 2 1 2 5 2 3 3 ...
## $ Attrition : Factor w/ 2 levels "No","Yes": 2 1 2 1 1 1 1 1 1 1 ...
## $ BusinessTravel : Factor w/ 3 levels "Non-Travel","Travel_Frequently",..: 3 2 3 2 3 2 3 3 2 3 ...
## $ DailyRate : Factor w/ 5 levels "[102,392]","(392,656]",..: 4 1 5 5 2 4 5 5 1 5 ...
## $ Department : Factor w/ 3 levels "Human_Resources",..: 3 2 2 2 2 2 2 2 2 2 ...
## $ DistanceFromHome : Factor w/ 5 levels "[1,2]","(2,5]",..: 1 3 1 2 1 1 2 5 5 5 ...
## $ Education : Ord.factor w/ 5 levels "Below_College"<..: 2 1 2 4 1 2 3 1 3 3 ...
## $ EducationField : Factor w/ 6 levels "Human_Resources",..: 2 2 5 2 4 2 4 2 2 4 ...
## $ EnvironmentSatisfaction : Ord.factor w/ 4 levels "Low"<"Medium"<..: 2 3 4 4 1 4 3 4 4 3 ...
## $ Gender : Factor w/ 2 levels "Female","Male": 1 2 2 1 2 2 1 2 2 2 ...
## $ HourlyRate : Factor w/ 5 levels "[30,45]","(45,59]",..: 5 3 5 2 1 4 4 3 1 5 ...
## $ JobInvolvement : Ord.factor w/ 4 levels "Low"<"Medium"<..: 3 2 2 3 3 3 4 3 2 3 ...
## $ JobLevel : Factor w/ 5 levels "1","2","3","4",..: 2 2 1 1 1 1 1 1 3 2 ...
## $ JobRole : Factor w/ 9 levels "Healthcare_Representative",..: 8 7 3 7 3 3 3 3 5 1 ...
## $ JobSatisfaction : Ord.factor w/ 4 levels "Low"<"Medium"<..: 4 2 3 3 2 4 1 3 3 3 ...
## $ MaritalStatus : Factor w/ 3 levels "Divorced","Married",..: 3 2 3 2 2 3 2 1 3 2 ...
## $ MonthlyIncome : Factor w/ 5 levels "[1.01e+03,2.7e+03]",..: 4 3 1 2 2 2 1 1 4 3 ...
## $ MonthlyRate : Factor w/ 5 levels "[2.09e+03,6.89e+03]",..: 4 5 1 5 3 3 2 3 2 3 ...
## $ NumCompaniesWorked : Factor w/ 10 levels "0","1","2","3",..: 9 2 7 2 10 1 5 2 1 7 ...
## $ OverTime : Factor w/ 2 levels "No","Yes": 2 1 2 2 1 1 2 1 1 1 ...
## $ PercentSalaryHike : Factor w/ 5 levels "[11,12]","(12,13]",..: 1 5 3 1 1 2 5 5 5 2 ...
## $ PerformanceRating : Ord.factor w/ 4 levels "Low"<"Good"<"Excellent"<..: 3 4 3 3 3 3 4 4 4 3 ...
## $ RelationshipSatisfaction: Ord.factor w/ 4 levels "Low"<"Medium"<..: 1 4 2 3 4 3 1 2 2 2 ...
## $ StockOptionLevel : Factor w/ 4 levels "0","1","2","3": 1 2 1 1 2 1 4 2 1 3 ...
## $ TotalWorkingYears : Factor w/ 5 levels "[0,5]","(5,8]",..: 2 3 2 2 2 2 4 1 3 4 ...
## $ TrainingTimesLastYear : Factor w/ 7 levels "0","1","2","3",..: 1 4 4 4 4 3 4 3 3 4 ...
## $ WorkLifeBalance : Ord.factor w/ 4 levels "Bad"<"Good"<"Better"<..: 1 3 3 3 3 2 2 3 3 2 ...
## $ YearsAtCompany : Factor w/ 5 levels "[0,2]","(2,5]",..: 3 4 1 4 1 3 1 1 4 3 ...
## $ YearsInCurrentRole : Factor w/ 5 levels "[0,1]","(1,2]",..: 3 4 1 4 2 4 1 1 4 4 ...
## $ YearsSinceLastPromotion : Factor w/ 4 levels "Less than 1",..: 1 2 1 4 3 4 1 1 2 4 ...
## $ YearsWithCurrManager : Factor w/ 5 levels "[0,1]","(1,2]",..: 4 4 1 1 2 4 1 1 5 4 ...
newattrit <- attrition %>%
select_if(is.factor)
dim(newattrit)
## [1] 1470 31
Okay we have data on 1,470 employees. We have 30 potential predictor
(features) or independent variables and the all important attrition
variable which gives us a yes or no answer to the question of whether or
not the employee left. We’re to build the most accurate predictive model
we can that is also simple (parsimonious) and explainable. The
predictors we have seem to be the sorts of data we might have on hand in
our HR files and thank goodness are labelled in a way that makes them
pretty self explanatory.
Last post we explored the control options and built predictive models like the one below. For a review of what the output means and how CHAID works please refer back.
# explore the control options
ctrl <- chaid_control(minsplit = 200, minprob = 0.05)
ctrl
## $alpha2
## [1] 0.05
##
## $alpha3
## [1] -1
##
## $alpha4
## [1] 0.05
##
## $minsplit
## [1] 200
##
## $minbucket
## [1] 7
##
## $minprob
## [1] 0.05
##
## $stump
## [1] FALSE
##
## $maxheight
## [1] -1
##
## attr(,"class")
## [1] "chaid_control"
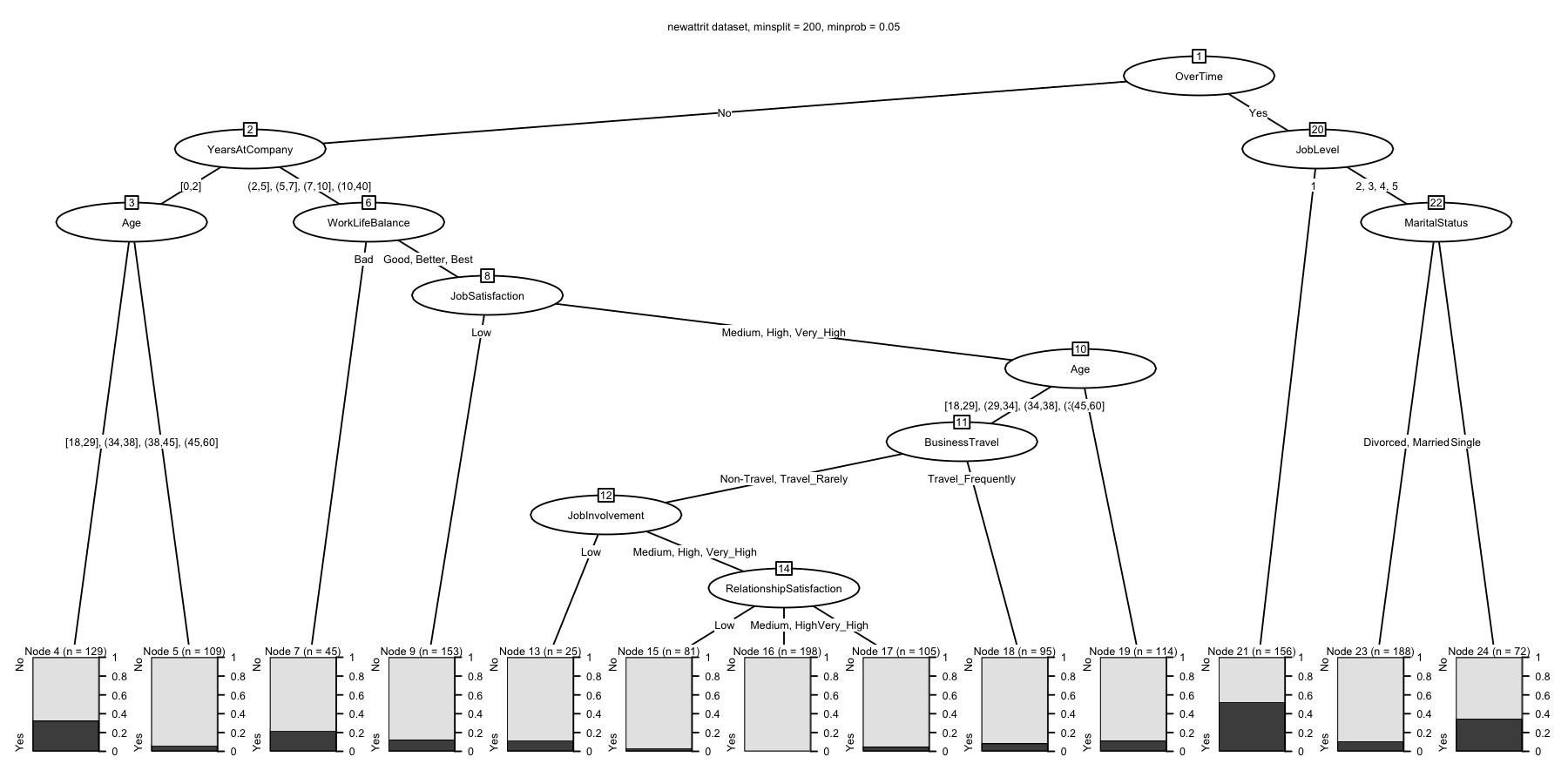
full_data <- chaid(Attrition ~ ., data = newattrit, control = ctrl)
print(full_data)
##
## Model formula:
## Attrition ~ Age + BusinessTravel + DailyRate + Department + DistanceFromHome +
## Education + EducationField + EnvironmentSatisfaction + Gender +
## HourlyRate + JobInvolvement + JobLevel + JobRole + JobSatisfaction +
## MaritalStatus + MonthlyIncome + MonthlyRate + NumCompaniesWorked +
## OverTime + PercentSalaryHike + PerformanceRating + RelationshipSatisfaction +
## StockOptionLevel + TotalWorkingYears + TrainingTimesLastYear +
## WorkLifeBalance + YearsAtCompany + YearsInCurrentRole + YearsSinceLastPromotion +
## YearsWithCurrManager
##
## Fitted party:
## [1] root
## | [2] OverTime in No
## | | [3] YearsAtCompany in [0,2]
## | | | [4] Age in [18,29], (29,34]: No (n = 129, err = 32.6%)
## | | | [5] Age in (34,38], (38,45], (45,60]: No (n = 109, err = 6.4%)
## | | [6] YearsAtCompany in (2,5], (5,7], (7,10], (10,40]
## | | | [7] WorkLifeBalance in Bad: No (n = 45, err = 22.2%)
## | | | [8] WorkLifeBalance in Good, Better, Best
## | | | | [9] JobSatisfaction in Low: No (n = 153, err = 12.4%)
## | | | | [10] JobSatisfaction in Medium, High, Very_High
## | | | | | [11] Age in [18,29], (29,34], (34,38], (38,45]
## | | | | | | [12] BusinessTravel in Non-Travel, Travel_Rarely
## | | | | | | | [13] JobInvolvement in Low: No (n = 25, err = 12.0%)
## | | | | | | | [14] JobInvolvement in Medium, High, Very_High
## | | | | | | | | [15] RelationshipSatisfaction in Low: No (n = 81, err = 3.7%)
## | | | | | | | | [16] RelationshipSatisfaction in Medium, High: No (n = 198, err = 0.0%)
## | | | | | | | | [17] RelationshipSatisfaction in Very_High: No (n = 105, err = 4.8%)
## | | | | | | [18] BusinessTravel in Travel_Frequently: No (n = 95, err = 8.4%)
## | | | | | [19] Age in (45,60]: No (n = 114, err = 11.4%)
## | [20] OverTime in Yes
## | | [21] JobLevel in 1: Yes (n = 156, err = 47.4%)
## | | [22] JobLevel in 2, 3, 4, 5
## | | | [23] MaritalStatus in Divorced, Married: No (n = 188, err = 10.6%)
## | | | [24] MaritalStatus in Single: No (n = 72, err = 34.7%)
##
## Number of inner nodes: 11
## Number of terminal nodes: 13
plot(
full_data,
main = "newattrit dataset, minsplit = 200, minprob = 0.05",
gp = gpar(
lty = "solid",
lwd = 2,
fontsize = 10
)
)
Over-fitting
Okay we have a working predictive model. At this point, however, we’ve
been cheating to a certain degree! We’ve been using every available
piece of data we have to develop the best possible model. We’ve told the
powerful all-knowing algorithims to squeeze every last bit of accuracy
they can out of the data. We’ve told it to fit the best possible
model. Problem is that we may have done that at the cost of being able
to generalize our model to new data or to new situations. That’s the
problem of over-fitting in a nutshell. If you want a fuller
understanding please consider reading this post on
EliteDataScience.
I’m going to move on to a solution for solving this limitation and
that’s where caret comes in.
We’re going to use caret to employ cross-validation a.k.a. cv to
solve this challenge for us, or more accurately to mitigate the problem.
The same article
explains
it well so I won’t repeat that explanation here, I’ll simply show you
how to run the steps in R.
This is also a good time to point out that caret has extraordinarily
comprehensive documentation which I
used extensively and I’m limiting myself to the basics.
As a first step, let’s just take 30% of our data and put is aside for a
minute. We’re not going to let chaid see it or know about it as we
build the model. In some scenarios you have subsequent data at hand for
checking your model (data from another company or another year or …). We
don’t, so we’re going to self-impose this restraint. Why 30%? Doesn’t
have to be, could be as low as 20% or as high as 40% it really depends
on how conservative you want to be, and how much data you have at hand.
Since this is just a tutorial we’ll simply use 30% as a representative
number. We’ve already loaded both rsample and caret either of which
is quite capable of making this split for us. I’m arbitrarily going to
use rsample syntax which is the line with initial_split(newattrit,
prop = .7, strata = "Attrition") in it. That takes our data set
newattrit makes a 70% split ensuring that we keep our outcome variable
Attrition as close to 70/30 as we can. This is important because our
data is already pretty lop-sided for outcomes. The two subsequent lines
serve to take the data contained in split and produce two separate
dataframes, test and train. They have 440 and 1030 staff members
each. We’ll set test aside for now and focus on train.
# Create training (70%) and test (30%) sets for the attrition data.
# Use set.seed for reproducibility
#####
set.seed(1234)
split <- initial_split(newattrit, prop = .7, strata = "Attrition")
train <- training(split)
test <- testing(split)
The next step is a little counter-intuitive but quite practical. Turns
out that many models do not perform well when you feed them a formula
for the model even if they claim to support a formula interface (as
CHAID does). Here’s an SO
link
that discusses in detail but my suggestion to you is to always separate
them and avoid the problem altogether. We’re just taking our
predictors or features and putting them in x while we put our
outcome in y.
# create response and feature data
features <- setdiff(names(train), "Attrition")
x <- train[, features]
y <- train$Attrition
Alright, let’s get back on track. trainControl is the function within
caret we need to use. Chapter 5 in the caret doco covers it in great
detail. I’m simply going to pluck out a few sane and safe options.
method = "cv" gets us cross-validation. number = 10 is pretty
obvious. I happen to like seeing the progress in case I want to go for
coffee so verboseIter = TRUE, and I play it safe and explicitly save
my predictions savePredictions = "final". We put everything in
train_control which we’ll use in a minute.
# set up 10-fold cross validation procedure
train_control <- trainControl(method = "cv",
number = 10,
verboseIter = TRUE,
savePredictions = "final")
Not surprisingly the train function in caret trains our model! It
wants to know what our x and y’s are, as well as our training
control parameters which we’ve parked in train_control. At this point
we could successfully unleash the dogs of war (sorry Shakespeare) and
train our model since we know we want to use chaid. But let’s change
one other useful thing and that is metric which is what metric we want
to use to pick the “best” model. Instead of the default “accuracy” we’ll
use Kappa which as you may remember from the last post is more
conservative measure of how well we did.
If you’re running this code yourself this is a good time to take a coffee break. I’ll tell you later how to find out how long it took more or less exactly. But there’s no getting around it we’re model building many more times so it takes longer.
# train model
chaid.m1 <- train(
x = x,
y = y,
method = "chaid",
metric = "Kappa",
trControl = train_control
)
## + Fold01: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold01: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold01: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold01: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold01: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold01: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold02: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold02: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold02: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold02: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold02: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold02: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold03: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold03: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold03: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold03: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold03: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold03: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold04: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold04: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold04: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold04: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold04: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold04: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold05: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold05: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold05: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold05: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold05: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold05: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold06: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold06: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold06: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold06: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold06: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold06: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold07: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold07: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold07: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold07: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold07: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold07: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold08: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold08: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold08: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold08: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold08: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold08: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold09: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold09: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold09: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold09: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold09: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold09: alpha2=0.01, alpha3=-1, alpha4=0.01
## + Fold10: alpha2=0.05, alpha3=-1, alpha4=0.05
## - Fold10: alpha2=0.05, alpha3=-1, alpha4=0.05
## + Fold10: alpha2=0.03, alpha3=-1, alpha4=0.03
## - Fold10: alpha2=0.03, alpha3=-1, alpha4=0.03
## + Fold10: alpha2=0.01, alpha3=-1, alpha4=0.01
## - Fold10: alpha2=0.01, alpha3=-1, alpha4=0.01
## Aggregating results
## Selecting tuning parameters
## Fitting alpha2 = 0.05, alpha3 = -1, alpha4 = 0.05 on full training set
And…. we’re done. Turns out in this case the best solution was what
chaid uses as defaults. The very last line of the output tells us
that. But let’s use what we have used in the past for printing and
plotting the results…
chaid.m1 #equivalent to print(chaid.m1)
## CHi-squared Automated Interaction Detection
##
## 1030 samples
## 30 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 928, 927, 927, 926, 928, 926, ...
## Resampling results across tuning parameters:
##
## alpha2 alpha4 Accuracy Kappa
## 0.01 0.01 0.8223292 0.1522392
## 0.03 0.03 0.8349699 0.1579585
## 0.05 0.05 0.8213958 0.1692826
##
## Tuning parameter 'alpha3' was held constant at a value of -1
## Kappa was used to select the optimal model using the largest value.
## The final values used for the model were alpha2 = 0.05, alpha3 = -1
## and alpha4 = 0.05.
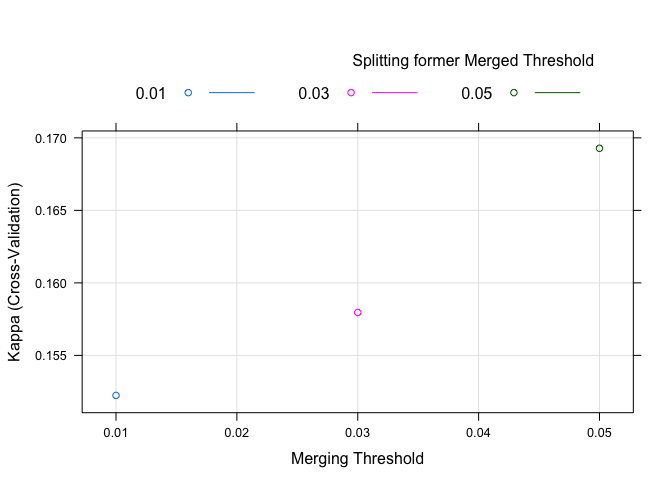
plot(chaid.m1)
Wait. What? These are not the output we’re used to. caret has changed
the output from its’ work (an improvement actually) but we’ll have to
change how we get the information out. Before we do that however, let’s
inspect what we have so far. The output gives us a nice concise summary.
1030 cases with 30 predictors. It gives us an idea of how many of the
1030 cases were used in the individual folds Summary of sample
sizes: 928, 927, 927, 926, 928, 926, ....
The bit about alpha2, alpha4, and alpha3 is somewhat mysterious.
We saw those names when we looked at the chaid_control documentation
last post but why are they here? We’ll come back to that in a moment.
But it is clear that it thought Kappa of 0.1692826 was best.
The plot isn’t what we’re used to seeing, but is easy to understand.
Kappa is on the y axis, alpha2 on the x axis and it’s shaded/colored
by alpha4 (remember we left alpha3 out of the mix). The plot is a
bit of overkill for what we did but we’ll put it to better use later.
But what about the things we were used to seeing? Well if you remember
that caret is reporting averages of all the folds it sort of makes
sense that the best final model results are now in
chaid.m1$finalModel so we need to use that when we print or plot.
So in the next block of code let’s:
- Print the final model from
chaid(chaid.m1$finalModel) - Plot the final model from
chaid(plot(chaid.m1$finalModel)) - Produce the
confusionMatrixacross all folds (confusionMatrix(chaid.m1)) - Produce the
confusionMatrixusing the final model (confusionMatrix(predict(chaid.m1), y)) - Check on variable importance (
varImp(chaid.m1)) - The best tuning parameters are stored in
chaid.m1$bestTune - How long did it take? Look in
chaid.m1$times - In case you forgot what method you used look here
chaid.m1$method - We’ll look at model info in a bit
chaid.m1$modelInfo - The summarized results are here in a nice format if needed later
chaid.m1$results
Many of these you’ll never need but I wanted to at least give you a hint
of how complete the chaid.m1 object is
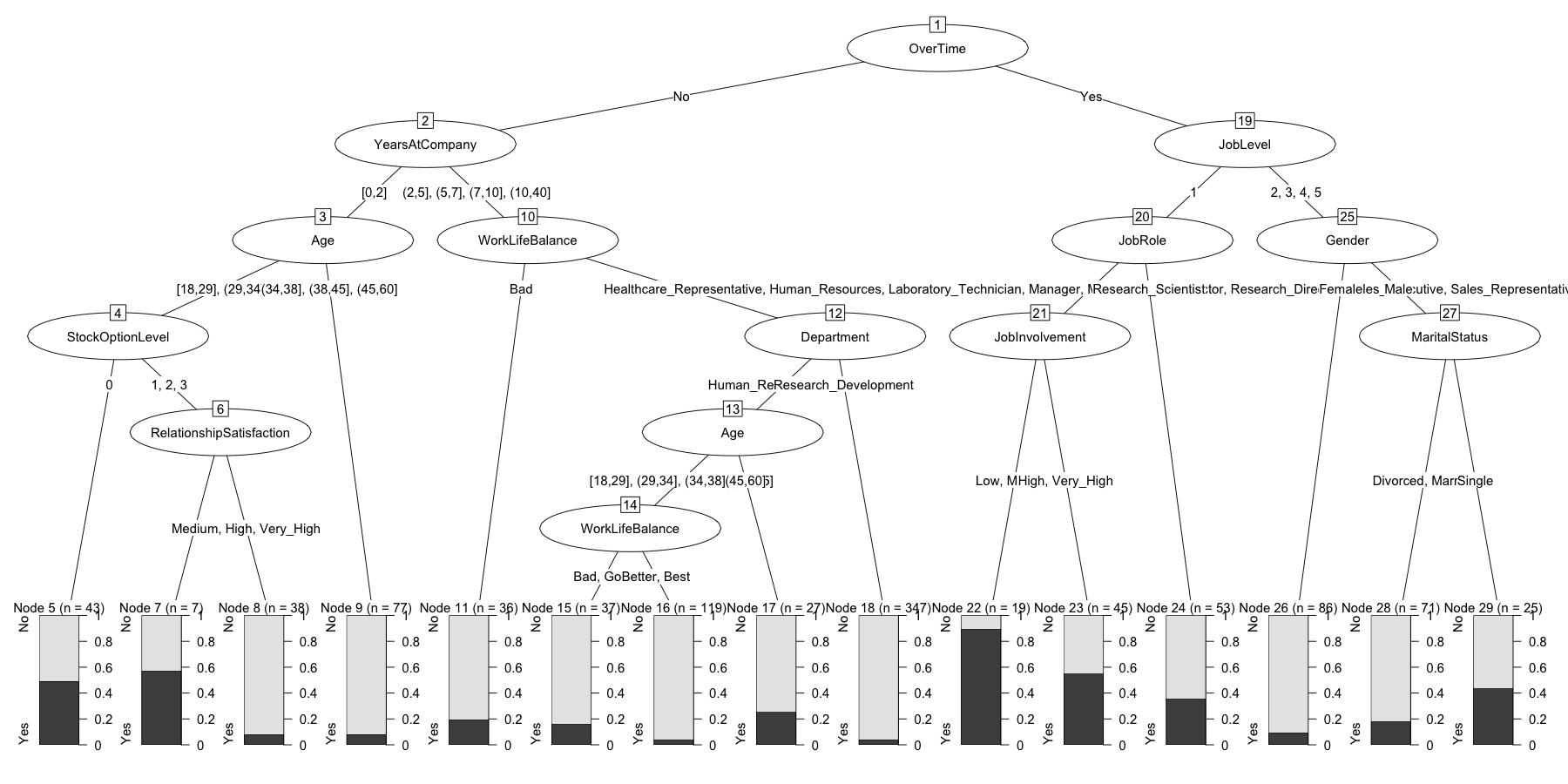
chaid.m1$finalModel
##
## Model formula:
## .outcome ~ Age + BusinessTravel + DailyRate + Department + DistanceFromHome +
## Education + EducationField + EnvironmentSatisfaction + Gender +
## HourlyRate + JobInvolvement + JobLevel + JobRole + JobSatisfaction +
## MaritalStatus + MonthlyIncome + MonthlyRate + NumCompaniesWorked +
## OverTime + PercentSalaryHike + PerformanceRating + RelationshipSatisfaction +
## StockOptionLevel + TotalWorkingYears + TrainingTimesLastYear +
## WorkLifeBalance + YearsAtCompany + YearsInCurrentRole + YearsSinceLastPromotion +
## YearsWithCurrManager
##
## Fitted party:
## [1] root
## | [2] OverTime in No
## | | [3] YearsAtCompany in [0,2]
## | | | [4] Age in [18,29], (29,34]
## | | | | [5] StockOptionLevel in 0: No (n = 43, err = 48.8%)
## | | | | [6] StockOptionLevel in 1, 2, 3
## | | | | | [7] RelationshipSatisfaction in Low: Yes (n = 7, err = 42.9%)
## | | | | | [8] RelationshipSatisfaction in Medium, High, Very_High: No (n = 38, err = 7.9%)
## | | | [9] Age in (34,38], (38,45], (45,60]: No (n = 77, err = 7.8%)
## | | [10] YearsAtCompany in (2,5], (5,7], (7,10], (10,40]
## | | | [11] WorkLifeBalance in Bad: No (n = 36, err = 19.4%)
## | | | [12] WorkLifeBalance in Good, Better, Best
## | | | | [13] Department in Human_Resources, Sales
## | | | | | [14] Age in [18,29], (29,34], (34,38], (38,45]
## | | | | | | [15] WorkLifeBalance in Bad, Good: No (n = 37, err = 16.2%)
## | | | | | | [16] WorkLifeBalance in Better, Best: No (n = 119, err = 4.2%)
## | | | | | [17] Age in (45,60]: No (n = 27, err = 25.9%)
## | | | | [18] Department in Research_Development: No (n = 347, err = 4.0%)
## | [19] OverTime in Yes
## | | [20] JobLevel in 1
## | | | [21] JobRole in Healthcare_Representative, Human_Resources, Laboratory_Technician, Manager, Manufacturing_Director, Research_Director, Sales_Executive, Sales_Representative
## | | | | [22] JobInvolvement in Low, Medium: Yes (n = 19, err = 10.5%)
## | | | | [23] JobInvolvement in High, Very_High: Yes (n = 45, err = 44.4%)
## | | | [24] JobRole in Research_Scientist: No (n = 53, err = 35.8%)
## | | [25] JobLevel in 2, 3, 4, 5
## | | | [26] Gender in Female: No (n = 86, err = 9.3%)
## | | | [27] Gender in Male
## | | | | [28] MaritalStatus in Divorced, Married: No (n = 71, err = 18.3%)
## | | | | [29] MaritalStatus in Single: No (n = 25, err = 44.0%)
##
## Number of inner nodes: 14
## Number of terminal nodes: 15
plot(chaid.m1$finalModel)
confusionMatrix(chaid.m1)
## Cross-Validated (10 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 79.0 13.0
## Yes 4.9 3.1
##
## Accuracy (average) : 0.8214
confusionMatrix(predict(chaid.m1), y)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 839 120
## Yes 25 46
##
## Accuracy : 0.8592
## 95% CI : (0.8365, 0.8799)
## No Information Rate : 0.8388
## P-Value [Acc > NIR] : 0.03938
##
## Kappa : 0.3228
## Mcnemar's Test P-Value : 5.89e-15
##
## Sensitivity : 0.9711
## Specificity : 0.2771
## Pos Pred Value : 0.8749
## Neg Pred Value : 0.6479
## Prevalence : 0.8388
## Detection Rate : 0.8146
## Detection Prevalence : 0.9311
## Balanced Accuracy : 0.6241
##
## 'Positive' Class : No
##
varImp(chaid.m1)
## ROC curve variable importance
##
## only 20 most important variables shown (out of 30)
##
## Importance
## OverTime 100.00
## YearsInCurrentRole 90.81
## YearsAtCompany 90.41
## MonthlyIncome 87.08
## JobLevel 84.36
## TotalWorkingYears 80.04
## YearsWithCurrManager 79.78
## StockOptionLevel 69.51
## MaritalStatus 65.96
## Age 59.31
## JobSatisfaction 44.86
## JobInvolvement 44.27
## DistanceFromHome 36.80
## EnvironmentSatisfaction 32.15
## WorkLifeBalance 31.63
## DailyRate 30.23
## JobRole 29.94
## NumCompaniesWorked 28.67
## Department 25.79
## HourlyRate 19.81
chaid.m1$bestTune
## alpha2 alpha3 alpha4
## 3 0.05 -1 0.05
chaid.m1$times
## $everything
## user system elapsed
## 247.218 1.581 248.999
##
## $final
## user system elapsed
## 9.612 0.055 9.674
##
## $prediction
## [1] NA NA NA
chaid.m1$method
## [1] "chaid"
chaid.m1$modelInfo
## $label
## [1] "CHi-squared Automated Interaction Detection"
##
## $library
## [1] "CHAID"
##
## $loop
## NULL
##
## $type
## [1] "Classification"
##
## $parameters
## parameter class
## 1 alpha2 numeric
## 2 alpha3 numeric
## 3 alpha4 numeric
## label
## 1 Merging Threshold
## 2 Splitting former Merged Threshold
## 3 \n Splitting former Merged Threshold
##
## $grid
## function (x, y, len = NULL, search = "grid")
## {
## if (search == "grid") {
## out <- data.frame(alpha2 = seq(from = 0.05, to = 0.01,
## length = len), alpha3 = -1, alpha4 = seq(from = 0.05,
## to = 0.01, length = len))
## }
## else {
## out <- data.frame(alpha2 = runif(len, min = 1e-06, max = 0.1),
## alpha3 = runif(len, min = -0.1, max = 0.1), alpha4 = runif(len,
## min = 1e-06, max = 0.1))
## }
## out
## }
##
## $fit
## function (x, y, wts, param, lev, last, classProbs, ...)
## {
## dat <- if (is.data.frame(x))
## x
## else as.data.frame(x)
## dat$.outcome <- y
## theDots <- list(...)
## if (any(names(theDots) == "control")) {
## theDots$control$alpha2 <- param$alpha2
## theDots$control$alpha3 <- param$alpha3
## theDots$control$alpha4 <- param$alpha4
## ctl <- theDots$control
## theDots$control <- NULL
## }
## else ctl <- chaid_control(alpha2 = param$alpha2, alpha3 = param$alpha3,
## alpha4 = param$alpha4)
## if (!is.null(wts))
## theDots$weights <- wts
## modelArgs <- c(list(formula = as.formula(".outcome ~ ."),
## data = dat, control = ctl), theDots)
## out <- do.call(CHAID::chaid, modelArgs)
## out
## }
## <bytecode: 0x7ff7fd0b48a8>
##
## $predict
## function (modelFit, newdata, submodels = NULL)
## {
## if (!is.data.frame(newdata))
## newdata <- as.data.frame(newdata)
## predict(modelFit, newdata)
## }
## <bytecode: 0x7ff7f6851190>
##
## $prob
## function (modelFit, newdata, submodels = NULL)
## {
## if (!is.data.frame(newdata))
## newdata <- as.data.frame(newdata)
## predict(modelFit, newdata, type = "prob")
## }
##
## $levels
## function (x)
## x$obsLevels
##
## $predictors
## function (x, surrogate = TRUE, ...)
## {
## predictors(terms(x))
## }
##
## $tags
## [1] "Tree-Based Model" "Implicit Feature Selection"
## [3] "Two Class Only" "Accepts Case Weights"
##
## $sort
## function (x)
## x[order(-x$alpha2, -x$alpha4, -x$alpha3), ]
chaid.m1$results
## alpha2 alpha3 alpha4 Accuracy Kappa AccuracySD KappaSD
## 1 0.01 -1 0.01 0.8223292 0.1522392 0.01887938 0.1278739
## 2 0.03 -1 0.03 0.8349699 0.1579585 0.02503052 0.1093852
## 3 0.05 -1 0.05 0.8213958 0.1692826 0.03353654 0.1180522
Let’s tune it up a little
Having mastered the basics of using caret and chaid let’s explore a
little deeper. By default caret allows us to adjust three parameters
in our chaid model; alpha2, alpha3, and alpha4. As a matter of
fact it will allow us to build a grid of those parameters and test all
the permutations we like, using the same cross-validation process. I’m a
bit worried that we’re not being conservative enough. I’d like to train
our model using p values for alpha that are not .05, .03, and .01 but
instead the de facto levels in my discipline; .05, .01, and .001. The
function in caret is tuneGrid. We’ll use the base R function
expand.grid to build a dataframe with all the combinations and then
feed it to caret in our next training.
Therefore search_grid will hold the values and we’ll add the line
tuneGrid = search_grid to our call to train. We’ll call the results
chaid.m2 and see how we did (I’m turning off verbose iteration output
since you’ve seen it on screen once already)…
# set up tuning grid default
search_grid <- expand.grid(
alpha2 = c(.05, .01, .001),
alpha4 = c(.05, .01, .001),
alpha3 = -1
)
# no verbose
train_control <- trainControl(method = "cv",
number = 10,
savePredictions = "final")
# train model
chaid.m2 <- train(
x = x,
y = y,
method = "chaid",
metric = "Kappa",
trControl = train_control,
tuneGrid = search_grid
)
chaid.m2
## CHi-squared Automated Interaction Detection
##
## 1030 samples
## 30 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 926, 927, 928, 928, 928, 926, ...
## Resampling results across tuning parameters:
##
## alpha2 alpha4 Accuracy Kappa
## 0.001 0.001 0.8378522 0.2755221
## 0.001 0.010 0.8329691 0.2039261
## 0.001 0.050 0.8231655 0.2026735
## 0.010 0.001 0.8378522 0.2755221
## 0.010 0.010 0.8358914 0.2185542
## 0.010 0.050 0.8280863 0.2231160
## 0.050 0.001 0.8407648 0.2992935
## 0.050 0.010 0.8387949 0.2487845
## 0.050 0.050 0.8280296 0.2324447
##
## Tuning parameter 'alpha3' was held constant at a value of -1
## Kappa was used to select the optimal model using the largest value.
## The final values used for the model were alpha2 = 0.05, alpha3 = -1
## and alpha4 = 0.001.
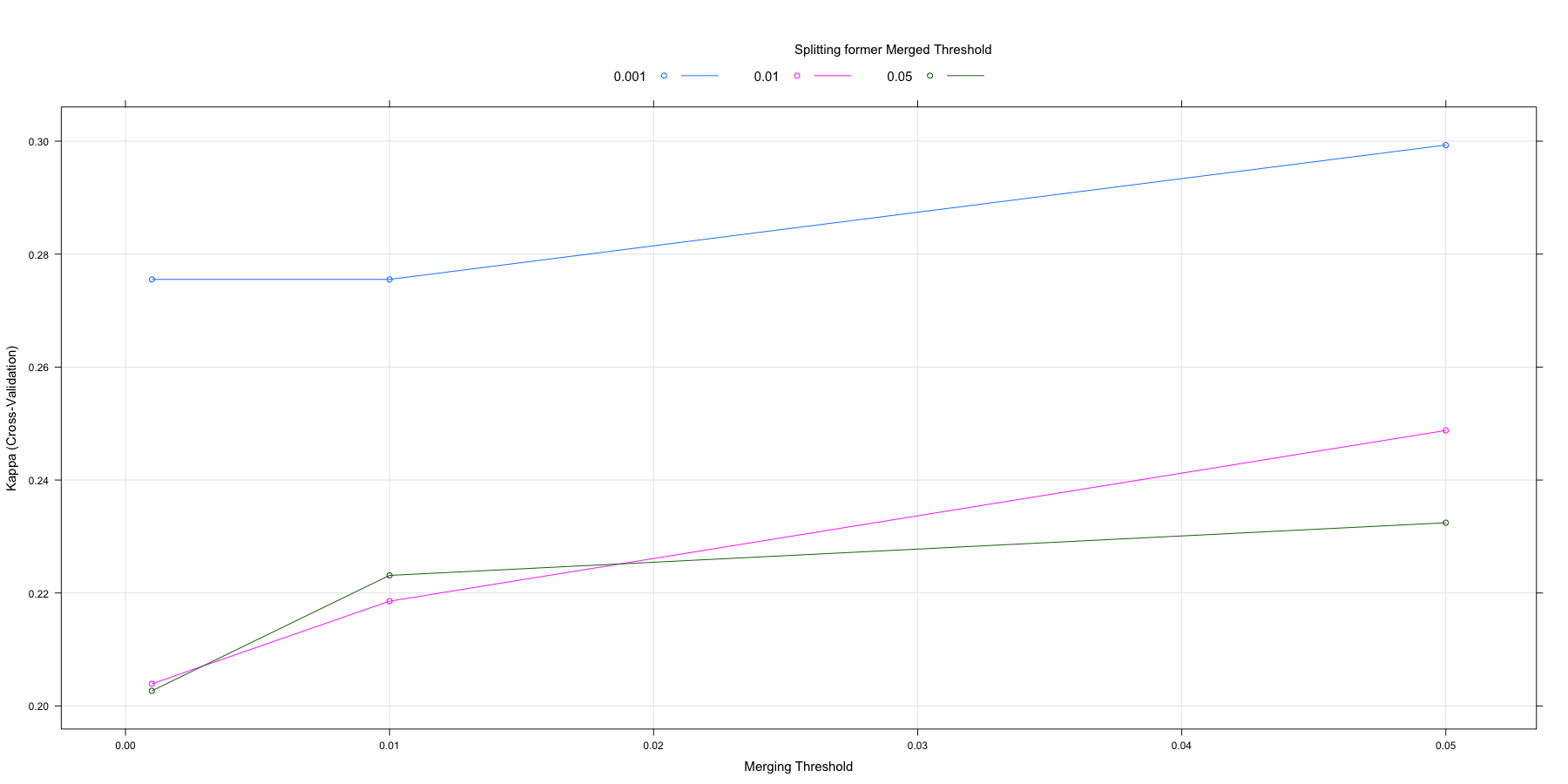
plot(chaid.m2)
chaid.m2$finalModel
##
## Model formula:
## .outcome ~ Age + BusinessTravel + DailyRate + Department + DistanceFromHome +
## Education + EducationField + EnvironmentSatisfaction + Gender +
## HourlyRate + JobInvolvement + JobLevel + JobRole + JobSatisfaction +
## MaritalStatus + MonthlyIncome + MonthlyRate + NumCompaniesWorked +
## OverTime + PercentSalaryHike + PerformanceRating + RelationshipSatisfaction +
## StockOptionLevel + TotalWorkingYears + TrainingTimesLastYear +
## WorkLifeBalance + YearsAtCompany + YearsInCurrentRole + YearsSinceLastPromotion +
## YearsWithCurrManager
##
## Fitted party:
## [1] root
## | [2] OverTime in No
## | | [3] YearsAtCompany in [0,2]: No (n = 165, err = 20.6%)
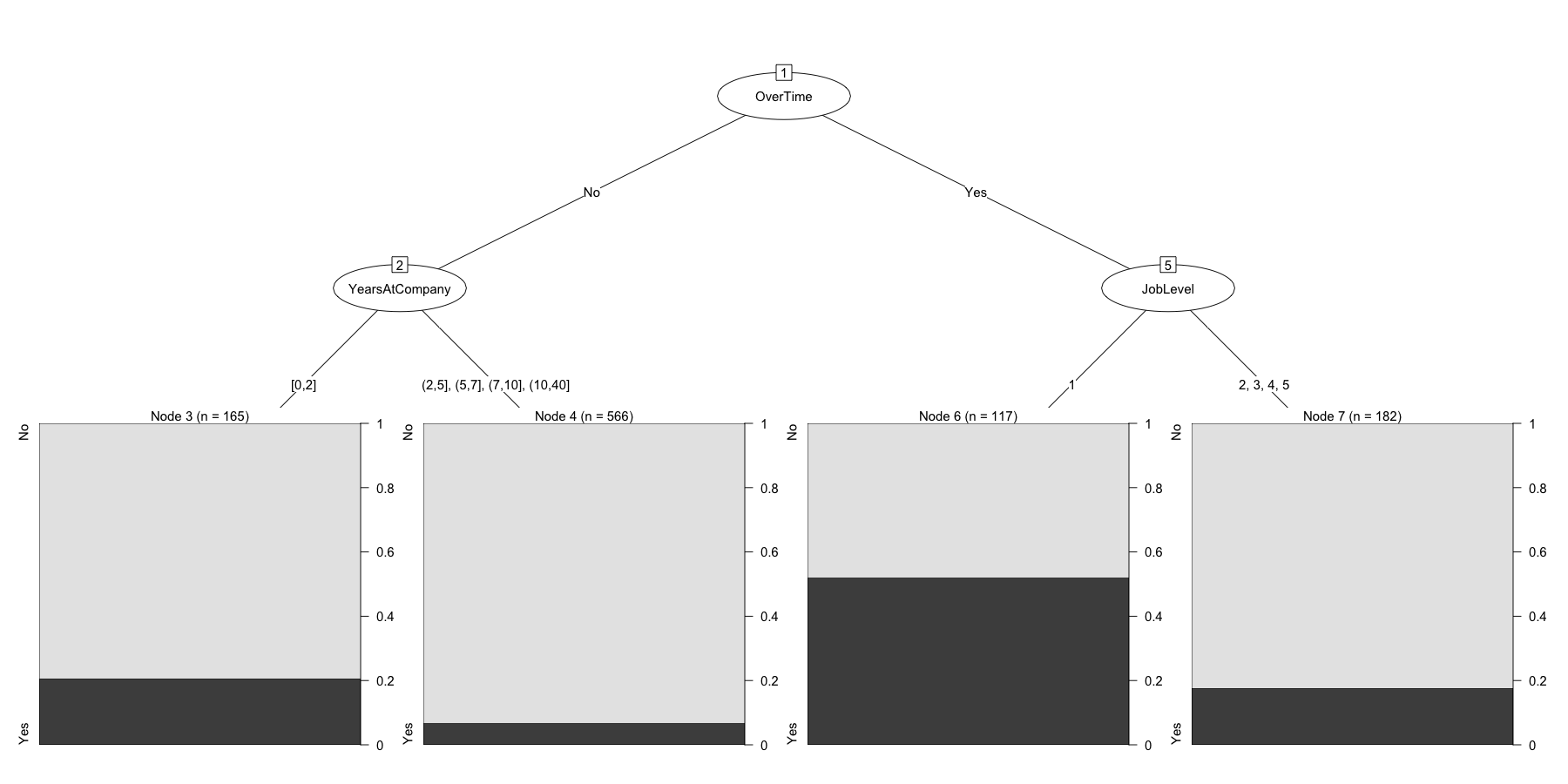
## | | [4] YearsAtCompany in (2,5], (5,7], (7,10], (10,40]: No (n = 566, err = 6.9%)
## | [5] OverTime in Yes
## | | [6] JobLevel in 1: Yes (n = 117, err = 47.9%)
## | | [7] JobLevel in 2, 3, 4, 5: No (n = 182, err = 17.6%)
##
## Number of inner nodes: 3
## Number of terminal nodes: 4
plot(chaid.m2$finalModel)
confusionMatrix(chaid.m2)
## Cross-Validated (10 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 79.0 11.1
## Yes 4.9 5.0
##
## Accuracy (average) : 0.8408
confusionMatrix(predict(chaid.m2), y)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 808 105
## Yes 56 61
##
## Accuracy : 0.8437
## 95% CI : (0.82, 0.8653)
## No Information Rate : 0.8388
## P-Value [Acc > NIR] : 0.354533
##
## Kappa : 0.3436
## Mcnemar's Test P-Value : 0.000155
##
## Sensitivity : 0.9352
## Specificity : 0.3675
## Pos Pred Value : 0.8850
## Neg Pred Value : 0.5214
## Prevalence : 0.8388
## Detection Rate : 0.7845
## Detection Prevalence : 0.8864
## Balanced Accuracy : 0.6513
##
## 'Positive' Class : No
##
chaid.m2$times
## $everything
## user system elapsed
## 524.972 3.729 529.873
##
## $final
## user system elapsed
## 2.173 0.013 2.191
##
## $prediction
## [1] NA NA NA
chaid.m2$results
## alpha2 alpha4 alpha3 Accuracy Kappa AccuracySD KappaSD
## 1 0.001 0.001 -1 0.8378522 0.2755221 0.02253555 0.09552095
## 2 0.001 0.010 -1 0.8329691 0.2039261 0.02263752 0.09977861
## 3 0.001 0.050 -1 0.8231655 0.2026735 0.03187552 0.12676157
## 4 0.010 0.001 -1 0.8378522 0.2755221 0.02253555 0.09552095
## 5 0.010 0.010 -1 0.8358914 0.2185542 0.02240334 0.10717030
## 6 0.010 0.050 -1 0.8280863 0.2231160 0.03056971 0.08137926
## 7 0.050 0.001 -1 0.8407648 0.2992935 0.02523390 0.10729121
## 8 0.050 0.010 -1 0.8387949 0.2487845 0.02277103 0.10696016
## 9 0.050 0.050 -1 0.8280296 0.2324447 0.03157911 0.13890292
Very nice! Some key points here. Even though our model got more
conservative and has far fewer nodes, our accuracy has improved as
measured both by traditional accuracy and Kappa. That applies at both
the average fold level but more importantly at the best model
prediction stage. Later on we’ll start using our models to predict
against the data we held out in test.
The plot is also more useful now. No matter what we do with alpha2 it
pays to keep alpha4 conservative at .001 (blue line always on top) but
keeping alpha2 modest seems to be best.
This goes to the heart of our conversation about over-fitting. While it may seem like 1,400+ cases is a lot of data we are at great risk of over-fitting if we try and build too complex a model, so sometimes a conservative track is warranted.
A Custom caret model
Earlier I printed the results of chaid.m1$modelInfo and then pretty
much skipped over discussing them. Under the covers one of the strengths
of caret is that it keeps some default information about how to tune
various types of algorithms. They are visible at
https://github.com/topepo/caret/tree/master/models/files.
My experience is that they are quite comprehensive and allow you to get
your modelling done. But sometimes you want to do something your own way
or different and caret has provisions for that. If you look at the
default model setup for CHAID here on
GITHUB
you can see that it only allows you to tune on alpha2, alpha3, and
alpha4 by default. That is not a comprehensive list of all the
parameters we can work with in chaid_control see ?chaid_control for
a listing and brief description of what they all are.
What if, for example, we wanted to tune based upon minsplit,
minbucket, minprob, maxheight instead? How would we go about using
all the built in functionality in caret but have it our way? There’s a
section in the caret documentation called “Using Your Own Model In
Train”
that does a great job of walking you through the steps. At first it
looked a little too complicated for my tastes, but I found that with a
bit of trial and error I was able to hack up the existing list that I
found on GITHUB and convert it into a list in my local environment that
worked perfectly for my needs.
I won’t bore you with all the details and the documentation is quite
good so it wound up being mainly a search and replace operation and
adding one parameter. I decided to call my version cgpCHAID and here’s
what the version looks like.
# hack up my own
cgpCHAID <- list(label = "CGP CHAID",
library = "CHAID",
loop = NULL,
type = c("Classification"),
parameters = data.frame(parameter = c('minsplit', 'minbucket', 'minprob', 'maxheight'),
class = rep('numeric', 4),
label = c('Numb obs in response where no further split',
"Minimum numb obs in terminal nodes",
"Minimum freq of obs in terminal nodes.",
"Maximum height for the tree")
),
grid = function(x, y, len = NULL, search = "grid") {
if(search == "grid") {
out <- data.frame(minsplit = c(20,30),
minbucket = 7,
minprob = c(0.05,0.01),
maxheight = -1)
} else {
out <- data.frame(minsplit = c(20,30),
minbucket = 7,
minprob = c(0.05,0.01),
maxheight = -1)
}
out
},
fit = function(x, y, wts, param, lev, last, classProbs, ...) {
dat <- if(is.data.frame(x)) x else as.data.frame(x)
dat$.outcome <- y
theDots <- list(...)
if(any(names(theDots) == "control")) {
theDots$control$minsplit <- param$minsplit
theDots$control$minbucket <- param$minbucket
theDots$control$minprob <- param$minprob
theDots$control$maxheight <- param$maxheight
ctl <- theDots$control
theDots$control <- NULL
} else ctl <- chaid_control(minsplit = param$minsplit,
minbucket = param$minbucket,
minprob = param$minprob,
maxheight = param$maxheight)
## pass in any model weights
if(!is.null(wts)) theDots$weights <- wts
modelArgs <- c(
list(
formula = as.formula(".outcome ~ ."),
data = dat,
control = ctl),
theDots)
out <- do.call(CHAID::chaid, modelArgs)
out
},
predict = function(modelFit, newdata, submodels = NULL) {
if(!is.data.frame(newdata)) newdata <- as.data.frame(newdata)
predict(modelFit, newdata)
},
prob = function(modelFit, newdata, submodels = NULL) {
if(!is.data.frame(newdata)) newdata <- as.data.frame(newdata)
predict(modelFit, newdata, type = "prob")
},
levels = function(x) x$obsLevels,
predictors = function(x, surrogate = TRUE, ...) {
predictors(terms(x))
},
tags = c('Tree-Based Model', "Implicit Feature Selection", "Two Class Only", "Accepts Case Weights"),
sort = function(x) x[order(-x$minsplit, -x$minbucket, -x$minprob, -x$maxheight),])
cgpCHAID
## $label
## [1] "CGP CHAID"
##
## $library
## [1] "CHAID"
##
## $loop
## NULL
##
## $type
## [1] "Classification"
##
## $parameters
## parameter class label
## 1 minsplit numeric Numb obs in response where no further split
## 2 minbucket numeric Minimum numb obs in terminal nodes
## 3 minprob numeric Minimum freq of obs in terminal nodes.
## 4 maxheight numeric Maximum height for the tree
##
## $grid
## function (x, y, len = NULL, search = "grid")
## {
## if (search == "grid") {
## out <- data.frame(minsplit = c(20, 30), minbucket = 7,
## minprob = c(0.05, 0.01), maxheight = -1)
## }
## else {
## out <- data.frame(minsplit = c(20, 30), minbucket = 7,
## minprob = c(0.05, 0.01), maxheight = -1)
## }
## out
## }
##
## $fit
## function (x, y, wts, param, lev, last, classProbs, ...)
## {
## dat <- if (is.data.frame(x))
## x
## else as.data.frame(x)
## dat$.outcome <- y
## theDots <- list(...)
## if (any(names(theDots) == "control")) {
## theDots$control$minsplit <- param$minsplit
## theDots$control$minbucket <- param$minbucket
## theDots$control$minprob <- param$minprob
## theDots$control$maxheight <- param$maxheight
## ctl <- theDots$control
## theDots$control <- NULL
## }
## else ctl <- chaid_control(minsplit = param$minsplit, minbucket = param$minbucket,
## minprob = param$minprob, maxheight = param$maxheight)
## if (!is.null(wts))
## theDots$weights <- wts
## modelArgs <- c(list(formula = as.formula(".outcome ~ ."),
## data = dat, control = ctl), theDots)
## out <- do.call(CHAID::chaid, modelArgs)
## out
## }
##
## $predict
## function (modelFit, newdata, submodels = NULL)
## {
## if (!is.data.frame(newdata))
## newdata <- as.data.frame(newdata)
## predict(modelFit, newdata)
## }
##
## $prob
## function (modelFit, newdata, submodels = NULL)
## {
## if (!is.data.frame(newdata))
## newdata <- as.data.frame(newdata)
## predict(modelFit, newdata, type = "prob")
## }
##
## $levels
## function (x)
## x$obsLevels
##
## $predictors
## function (x, surrogate = TRUE, ...)
## {
## predictors(terms(x))
## }
##
## $tags
## [1] "Tree-Based Model" "Implicit Feature Selection"
## [3] "Two Class Only" "Accepts Case Weights"
##
## $sort
## function (x)
## x[order(-x$minsplit, -x$minbucket, -x$minprob, -x$maxheight),
## ]
The final print statement shows what it looks like and confirms it is
there ready for us to use in the local environment. The original chaid
version in caret remains untouched and available in caret for when
we want it. To make use of our custom model we simply rebuild our search
grid using our new parameters.
# set up tuning grid cgpCHAID
search_grid <- expand.grid(
minsplit = c(30,40),
minprob = .1,
minbucket = 25,
maxheight = 4
)
search_grid
## minsplit minprob minbucket maxheight
## 1 30 0.1 25 4
## 2 40 0.1 25 4
Then to use it to train our third model chaid.m3 we insert it into the
method directive (not quoted because it’s in the local
environment).
# train model
chaid.m3 <- train(
x = x,
y = y,
method = cgpCHAID,
trControl = train_control,
metric = "Kappa",
tuneGrid = search_grid
)
The process runs for a few minutes and then produces output very similar
to what we received for chaid.m2. We get summarized information across
our 10 folds and the all important The final values used for the model
were minsplit = 40, minbucket = 25, minprob = 0.1 and maxheight = 4. I
won’t review all the details since I’ve already covered it I’ve simply
printed it out to confirm it all works.
chaid.m3
## CGP CHAID
##
## 1030 samples
## 30 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 926, 927, 927, 927, 927, 927, ...
## Resampling results across tuning parameters:
##
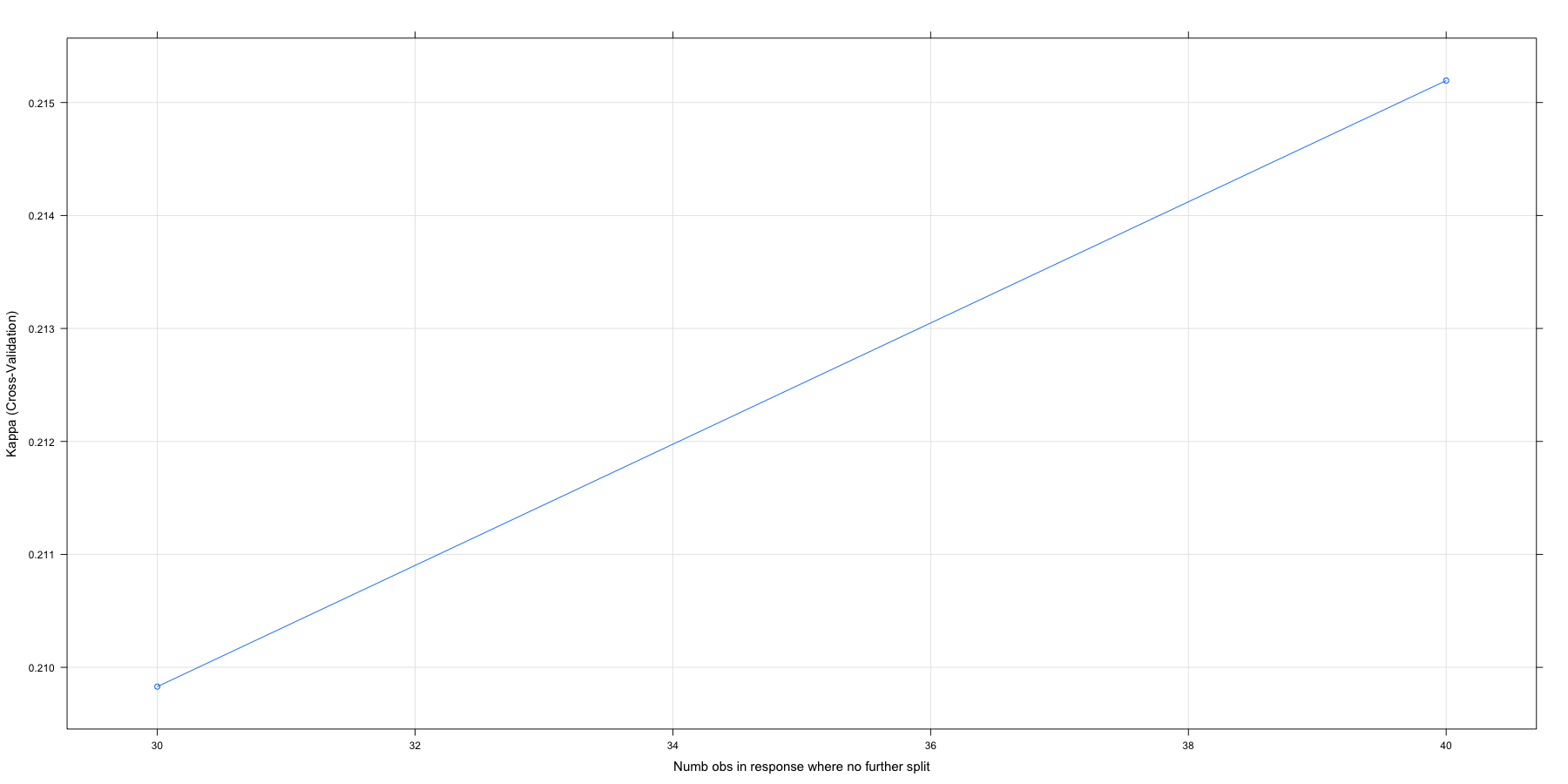
## minsplit Accuracy Kappa
## 30 0.8320546 0.2098294
## 40 0.8349672 0.2151947
##
## Tuning parameter 'minbucket' was held constant at a value of 25
##
## Tuning parameter 'minprob' was held constant at a value of 0.1
##
## Tuning parameter 'maxheight' was held constant at a value of 4
## Kappa was used to select the optimal model using the largest value.
## The final values used for the model were minsplit = 40, minbucket =
## 25, minprob = 0.1 and maxheight = 4.
chaid.m3$finalModel
##
## Model formula:
## .outcome ~ Age + BusinessTravel + DailyRate + Department + DistanceFromHome +
## Education + EducationField + EnvironmentSatisfaction + Gender +
## HourlyRate + JobInvolvement + JobLevel + JobRole + JobSatisfaction +
## MaritalStatus + MonthlyIncome + MonthlyRate + NumCompaniesWorked +
## OverTime + PercentSalaryHike + PerformanceRating + RelationshipSatisfaction +
## StockOptionLevel + TotalWorkingYears + TrainingTimesLastYear +
## WorkLifeBalance + YearsAtCompany + YearsInCurrentRole + YearsSinceLastPromotion +
## YearsWithCurrManager
##
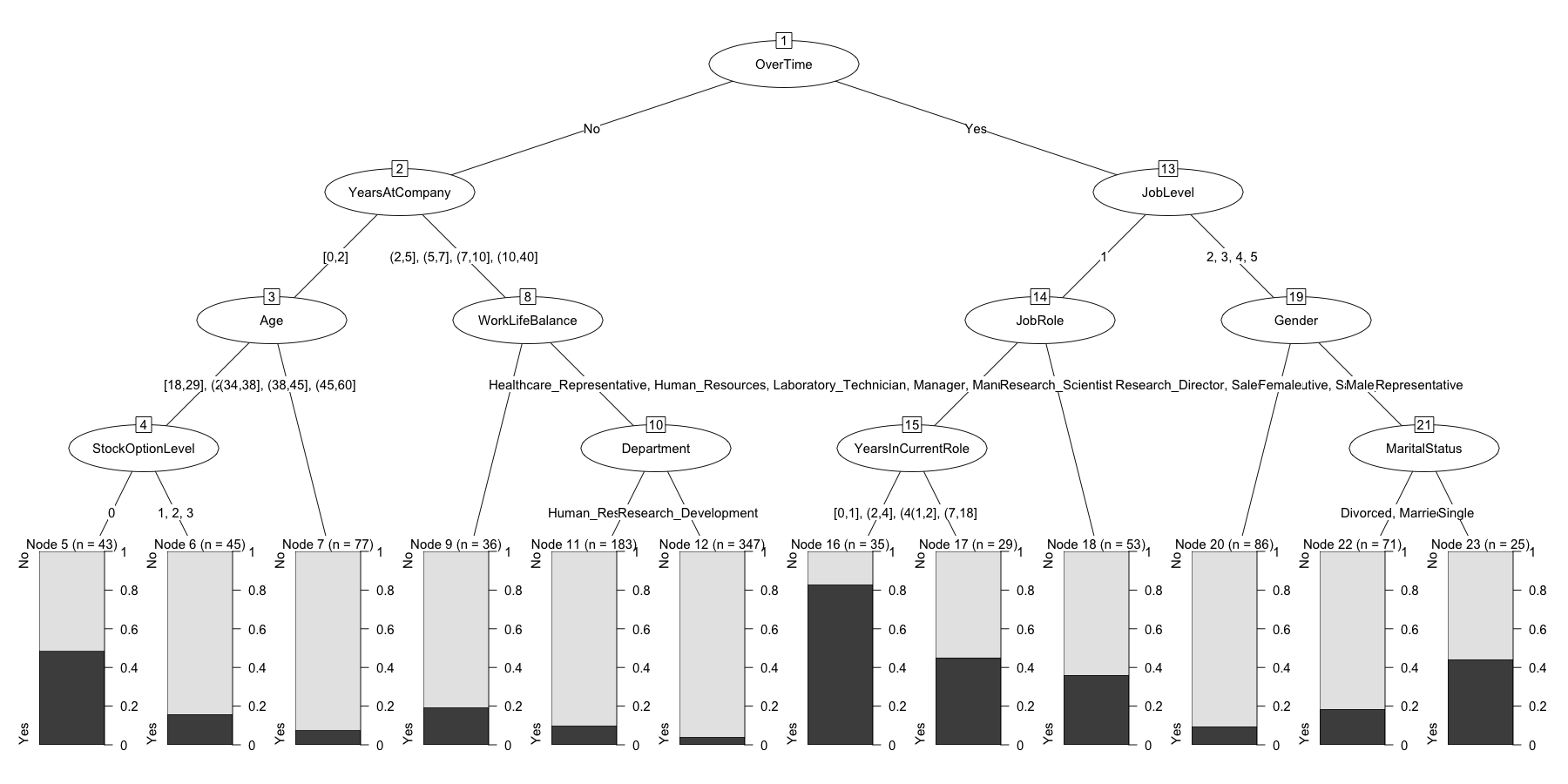
## Fitted party:
## [1] root
## | [2] OverTime in No
## | | [3] YearsAtCompany in [0,2]
## | | | [4] Age in [18,29], (29,34]
## | | | | [5] StockOptionLevel in 0: No (n = 43, err = 48.8%)
## | | | | [6] StockOptionLevel in 1, 2, 3: No (n = 45, err = 15.6%)
## | | | [7] Age in (34,38], (38,45], (45,60]: No (n = 77, err = 7.8%)
## | | [8] YearsAtCompany in (2,5], (5,7], (7,10], (10,40]
## | | | [9] WorkLifeBalance in Bad: No (n = 36, err = 19.4%)
## | | | [10] WorkLifeBalance in Good, Better, Best
## | | | | [11] Department in Human_Resources, Sales: No (n = 183, err = 9.8%)
## | | | | [12] Department in Research_Development: No (n = 347, err = 4.0%)
## | [13] OverTime in Yes
## | | [14] JobLevel in 1
## | | | [15] JobRole in Healthcare_Representative, Human_Resources, Laboratory_Technician, Manager, Manufacturing_Director, Research_Director, Sales_Executive, Sales_Representative
## | | | | [16] YearsInCurrentRole in [0,1], (2,4], (4,7]: Yes (n = 35, err = 17.1%)
## | | | | [17] YearsInCurrentRole in (1,2], (7,18]: No (n = 29, err = 44.8%)
## | | | [18] JobRole in Research_Scientist: No (n = 53, err = 35.8%)
## | | [19] JobLevel in 2, 3, 4, 5
## | | | [20] Gender in Female: No (n = 86, err = 9.3%)
## | | | [21] Gender in Male
## | | | | [22] MaritalStatus in Divorced, Married: No (n = 71, err = 18.3%)
## | | | | [23] MaritalStatus in Single: No (n = 25, err = 44.0%)
##
## Number of inner nodes: 11
## Number of terminal nodes: 12
confusionMatrix(chaid.m3)
## Cross-Validated (10 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 80.0 12.6
## Yes 3.9 3.5
##
## Accuracy (average) : 0.835
confusionMatrix(predict(chaid.m3), y)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 858 137
## Yes 6 29
##
## Accuracy : 0.8612
## 95% CI : (0.8385, 0.8817)
## No Information Rate : 0.8388
## P-Value [Acc > NIR] : 0.02656
##
## Kappa : 0.2463
## Mcnemar's Test P-Value : < 2e-16
##
## Sensitivity : 0.9931
## Specificity : 0.1747
## Pos Pred Value : 0.8623
## Neg Pred Value : 0.8286
## Prevalence : 0.8388
## Detection Rate : 0.8330
## Detection Prevalence : 0.9660
## Balanced Accuracy : 0.5839
##
## 'Positive' Class : No
##
plot(chaid.m3)
plot(chaid.m3$finalModel)
A quick reminder that you can get relative variable importance with
varImp. And of course the all important look at how well we predicted
against our held out test data set.
varImp(chaid.m3)
## ROC curve variable importance
##
## only 20 most important variables shown (out of 30)
##
## Importance
## OverTime 100.00
## YearsInCurrentRole 90.81
## YearsAtCompany 90.41
## MonthlyIncome 87.08
## JobLevel 84.36
## TotalWorkingYears 80.04
## YearsWithCurrManager 79.78
## StockOptionLevel 69.51
## MaritalStatus 65.96
## Age 59.31
## JobSatisfaction 44.86
## JobInvolvement 44.27
## DistanceFromHome 36.80
## EnvironmentSatisfaction 32.15
## WorkLifeBalance 31.63
## DailyRate 30.23
## JobRole 29.94
## NumCompaniesWorked 28.67
## Department 25.79
## HourlyRate 19.81
confusionMatrix(predict(chaid.m3, newdata = test), test$Attrition)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 365 67
## Yes 4 4
##
## Accuracy : 0.8386
## 95% CI : (0.8009, 0.8718)
## No Information Rate : 0.8386
## P-Value [Acc > NIR] : 0.5316
##
## Kappa : 0.0709
## Mcnemar's Test P-Value : 1.866e-13
##
## Sensitivity : 0.98916
## Specificity : 0.05634
## Pos Pred Value : 0.84491
## Neg Pred Value : 0.50000
## Prevalence : 0.83864
## Detection Rate : 0.82955
## Detection Prevalence : 0.98182
## Balanced Accuracy : 0.52275
##
## 'Positive' Class : No
##
One last exercise might also be fruitful. Suppose the only thing you
wanted to tell chaid was how deeply it was allowed to go in the tree.
Let’s run a simple example where we use all the defaults but force
either a two level or three level solution.
# set up tuning grid cgpCHAID
search_grid <- expand.grid(
minsplit = c(30),
minprob = .01,
minbucket = 7,
maxheight = 3:4
)
# train model
chaid.m4 <- train(
x = x,
y = y,
method = cgpCHAID,
metric = "Kappa",
trControl = train_control,
tuneGrid = search_grid
)
Those simple steps produce chaid.m4 which we can then investigate in
the usual way.
chaid.m4
## CGP CHAID
##
## 1030 samples
## 30 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 927, 926, 927, 926, 928, 927, ...
## Resampling results across tuning parameters:
##
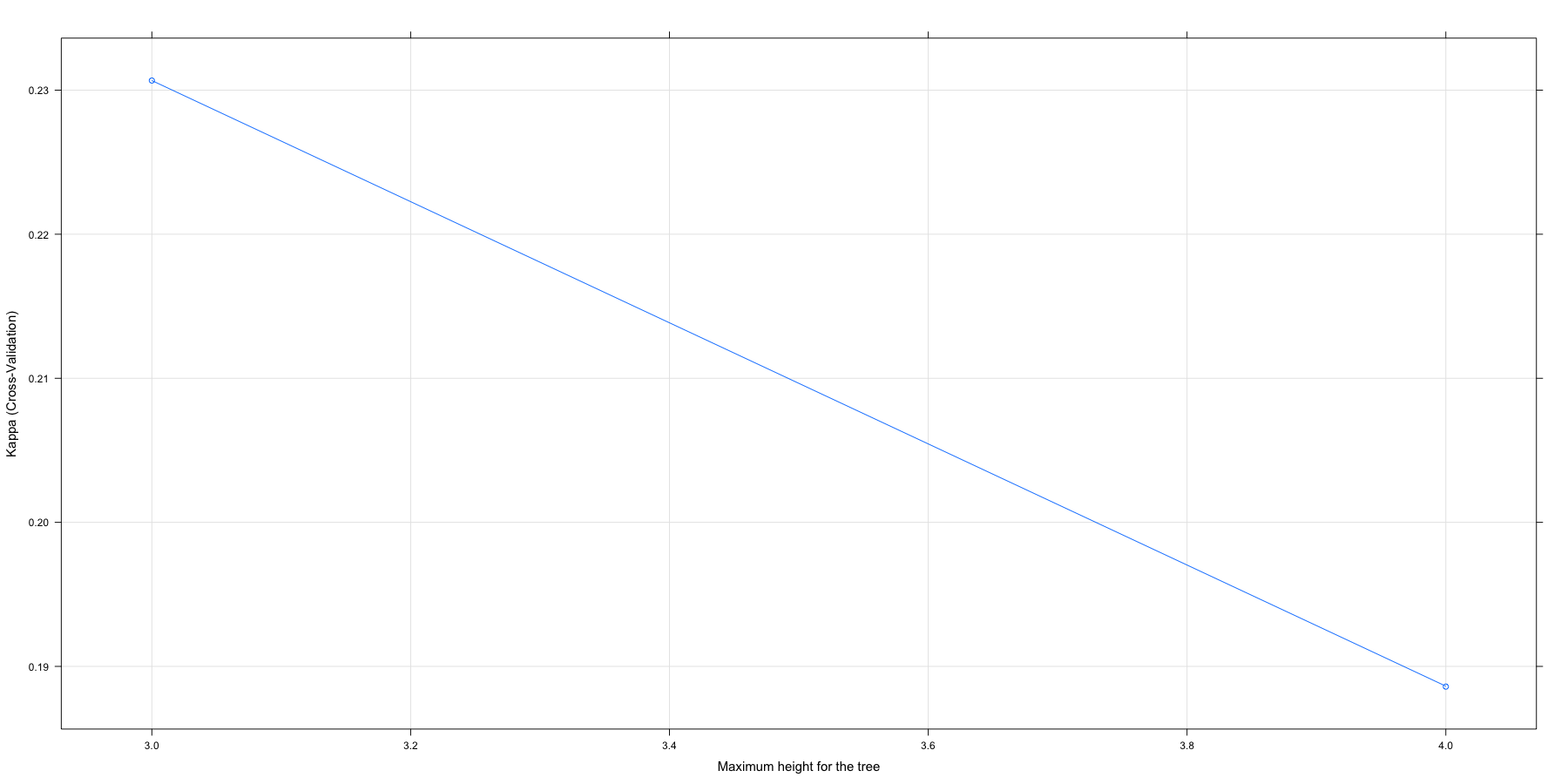
## maxheight Accuracy Kappa
## 3 0.8417388 0.2306686
## 4 0.8291923 0.1885956
##
## Tuning parameter 'minsplit' was held constant at a value of 30
##
## Tuning parameter 'minbucket' was held constant at a value of 7
##
## Tuning parameter 'minprob' was held constant at a value of 0.01
## Kappa was used to select the optimal model using the largest value.
## The final values used for the model were minsplit = 30, minbucket =
## 7, minprob = 0.01 and maxheight = 3.
chaid.m4$finalModel
##
## Model formula:
## .outcome ~ Age + BusinessTravel + DailyRate + Department + DistanceFromHome +
## Education + EducationField + EnvironmentSatisfaction + Gender +
## HourlyRate + JobInvolvement + JobLevel + JobRole + JobSatisfaction +
## MaritalStatus + MonthlyIncome + MonthlyRate + NumCompaniesWorked +
## OverTime + PercentSalaryHike + PerformanceRating + RelationshipSatisfaction +
## StockOptionLevel + TotalWorkingYears + TrainingTimesLastYear +
## WorkLifeBalance + YearsAtCompany + YearsInCurrentRole + YearsSinceLastPromotion +
## YearsWithCurrManager
##
## Fitted party:
## [1] root
## | [2] OverTime in No
## | | [3] YearsAtCompany in [0,2]
## | | | [4] Age in [18,29], (29,34]: No (n = 88, err = 31.8%)
## | | | [5] Age in (34,38], (38,45], (45,60]: No (n = 77, err = 7.8%)
## | | [6] YearsAtCompany in (2,5], (5,7], (7,10], (10,40]
## | | | [7] WorkLifeBalance in Bad: No (n = 36, err = 19.4%)
## | | | [8] WorkLifeBalance in Good, Better, Best: No (n = 530, err = 6.0%)
## | [9] OverTime in Yes
## | | [10] JobLevel in 1
## | | | [11] JobRole in Healthcare_Representative, Human_Resources, Laboratory_Technician, Manager, Manufacturing_Director, Research_Director, Sales_Executive, Sales_Representative: Yes (n = 64, err = 34.4%)
## | | | [12] JobRole in Research_Scientist: No (n = 53, err = 35.8%)
## | | [13] JobLevel in 2, 3, 4, 5
## | | | [14] Gender in Female: No (n = 86, err = 9.3%)
## | | | [15] Gender in Male: No (n = 96, err = 25.0%)
##
## Number of inner nodes: 7
## Number of terminal nodes: 8
confusionMatrix(chaid.m4)
## Cross-Validated (10 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 80.6 12.5
## Yes 3.3 3.6
##
## Accuracy (average) : 0.8417
confusionMatrix(predict(chaid.m4), y)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 842 124
## Yes 22 42
##
## Accuracy : 0.8583
## 95% CI : (0.8354, 0.879)
## No Information Rate : 0.8388
## P-Value [Acc > NIR] : 0.04743
##
## Kappa : 0.3027
## Mcnemar's Test P-Value : < 2e-16
##
## Sensitivity : 0.9745
## Specificity : 0.2530
## Pos Pred Value : 0.8716
## Neg Pred Value : 0.6563
## Prevalence : 0.8388
## Detection Rate : 0.8175
## Detection Prevalence : 0.9379
## Balanced Accuracy : 0.6138
##
## 'Positive' Class : No
##
plot(chaid.m4)
plot(chaid.m4$finalModel)
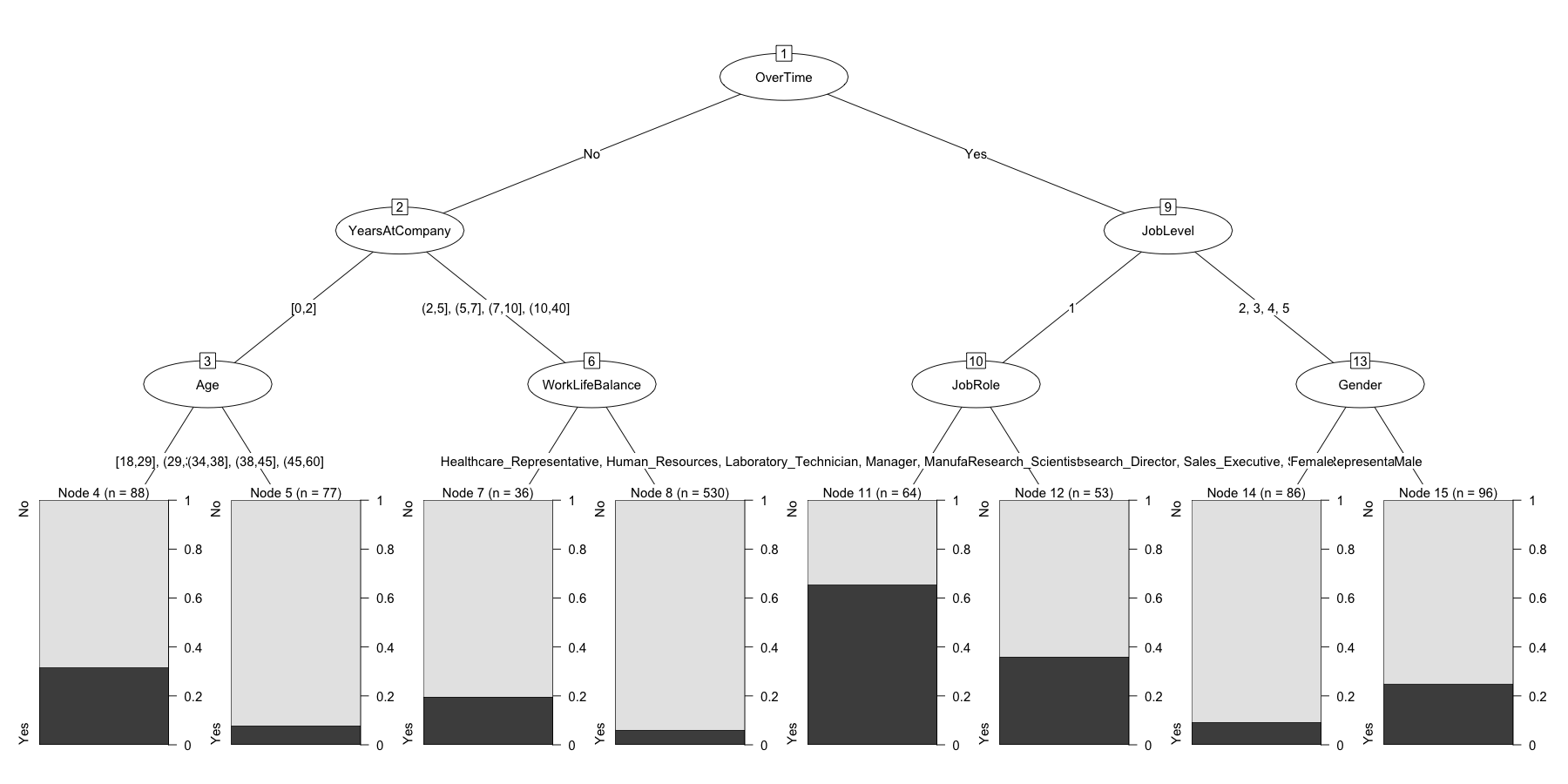
Although this post is more about explaining how to use the tools than it is about actually fitting this fictional data, let’s review all four of the models we built for comparative purposes. If you need to review what all these measures are please consult this webpage Confusion Matrix.
confusionMatrix(predict(chaid.m1, newdata = test), test$Attrition)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 357 64
## Yes 12 7
##
## Accuracy : 0.8273
## 95% CI : (0.7886, 0.8614)
## No Information Rate : 0.8386
## P-Value [Acc > NIR] : 0.7642
##
## Kappa : 0.0938
## Mcnemar's Test P-Value : 4.913e-09
##
## Sensitivity : 0.96748
## Specificity : 0.09859
## Pos Pred Value : 0.84798
## Neg Pred Value : 0.36842
## Prevalence : 0.83864
## Detection Rate : 0.81136
## Detection Prevalence : 0.95682
## Balanced Accuracy : 0.53304
##
## 'Positive' Class : No
##
confusionMatrix(predict(chaid.m2, newdata = test), test$Attrition)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 351 50
## Yes 18 21
##
## Accuracy : 0.8455
## 95% CI : (0.8082, 0.8779)
## No Information Rate : 0.8386
## P-Value [Acc > NIR] : 0.3779937
##
## Kappa : 0.3019
## Mcnemar's Test P-Value : 0.0001704
##
## Sensitivity : 0.9512
## Specificity : 0.2958
## Pos Pred Value : 0.8753
## Neg Pred Value : 0.5385
## Prevalence : 0.8386
## Detection Rate : 0.7977
## Detection Prevalence : 0.9114
## Balanced Accuracy : 0.6235
##
## 'Positive' Class : No
##
confusionMatrix(predict(chaid.m3, newdata = test), test$Attrition)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 365 67
## Yes 4 4
##
## Accuracy : 0.8386
## 95% CI : (0.8009, 0.8718)
## No Information Rate : 0.8386
## P-Value [Acc > NIR] : 0.5316
##
## Kappa : 0.0709
## Mcnemar's Test P-Value : 1.866e-13
##
## Sensitivity : 0.98916
## Specificity : 0.05634
## Pos Pred Value : 0.84491
## Neg Pred Value : 0.50000
## Prevalence : 0.83864
## Detection Rate : 0.82955
## Detection Prevalence : 0.98182
## Balanced Accuracy : 0.52275
##
## 'Positive' Class : No
##
confusionMatrix(predict(chaid.m4, newdata = test), test$Attrition)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 362 64
## Yes 7 7
##
## Accuracy : 0.8386
## 95% CI : (0.8009, 0.8718)
## No Information Rate : 0.8386
## P-Value [Acc > NIR] : 0.5316
##
## Kappa : 0.1178
## Mcnemar's Test P-Value : 3.012e-11
##
## Sensitivity : 0.98103
## Specificity : 0.09859
## Pos Pred Value : 0.84977
## Neg Pred Value : 0.50000
## Prevalence : 0.83864
## Detection Rate : 0.82273
## Detection Prevalence : 0.96818
## Balanced Accuracy : 0.53981
##
## 'Positive' Class : No
##
At this juncture we’re faced with the same problem we had in my last
post. We’re drowning in data from the individual confusionMatrix
results. We’ll resort to the same purrr
solution to give us a far
more legible table of results focusing on the metrics I’m most
interested in. To do that we need to:
- Make a
named listcalledmodellistthat contains our 4 models with a descriptive name for each - Use
mapfrompurrrto apply thepredictcommand to each model in turn to ourtestdataset - Pipe those results to a second
mapcommand to generate a confusion matrix comparing our predictions totest$Attritionwhich are the actual outcomes. - Pipe those results to a complex
map_dfr(that I explained last time) that creates a dataframe of all the results with each CHAID model as a row. - Show us the names of the columns we have available.
modellist <- list("Default tune" = chaid.m1,
"a2 & a4 stricter" = chaid.m2,
"Custom parameters" = chaid.m3,
"3 or 4 levels" = chaid.m4)
CHAIDResults <- map(modellist, ~ predict(.x, newdata = test)) %>%
map(~ confusionMatrix(test$Attrition, .x)) %>%
map_dfr(~ cbind(as.data.frame(t(.x$overall)),as.data.frame(t(.x$byClass))), .id = "ModelNumb")
names(CHAIDResults)
## [1] "ModelNumb" "Accuracy" "Kappa"
## [4] "AccuracyLower" "AccuracyUpper" "AccuracyNull"
## [7] "AccuracyPValue" "McnemarPValue" "Sensitivity"
## [10] "Specificity" "Pos Pred Value" "Neg Pred Value"
## [13] "Precision" "Recall" "F1"
## [16] "Prevalence" "Detection Rate" "Detection Prevalence"
## [19] "Balanced Accuracy"
From the list of available columns let’s use dplyr to select just the
columns we want, round the numeric columns to 3 digits and then use
kable to make a pretty table that is much easier to understand.
CHAIDResults %>%
select("ModelNumb", "Accuracy", "Kappa", "Sensitivity", "Specificity", "Neg Pred Value", "F1", "Balanced Accuracy") %>%
mutate_if(is.numeric,funs(round(.,3))) %>%
kable("html") %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))
| ModelNumb | Accuracy | Kappa | Sensitivity | Specificity | Neg Pred Value | F1 | Balanced Accuracy |
|---|---|---|---|---|---|---|---|
| Default tune | 0.827 | 0.094 | 0.848 | 0.368 | 0.099 | 0.904 | 0.608 |
| a2 & a4 stricter | 0.845 | 0.302 | 0.875 | 0.538 | 0.296 | 0.912 | 0.707 |
| Custom parameters | 0.839 | 0.071 | 0.845 | 0.500 | 0.056 | 0.911 | 0.672 |
| 3 or 4 levels | 0.839 | 0.118 | 0.850 | 0.500 | 0.099 | 0.911 | 0.675 |
By nearly every measure we care about, chaid.m2 (where the best fit was
alpha2 = 0.05 and alpha4 = 0.001) clearly emerges as the best predictor
against out test dataset. N.B. notice that if you only focus on
the default accuracy measure, the models are all very close. But if you
focus on more precise measures like Kappa and Negative Predictive Value
(which in this case is a great indicator of how well we are specifically
getting our prediction of attrition correct – compared to the more
common case of predicting that people will stay)
It’s a very simple and parsimonious model, where we only need to know
three things about the staff member to get pretty accurate predictions;
Overtime, YearsAtCompany, and JobLevel. It’s very clear that some
of the other variables may be at work here but we should acquire more
data to make that assessment rather than trying to overpredict with the
data we have on hand.
Done!
I hope you’ve found this useful. I am always open to comments, corrections and suggestions.
Chuck (ibecav at gmail dot com)
License

This
work is licensed under a
Creative
Commons Attribution-ShareAlike 4.0 International License.