CHAID v ranger v xgboost – a comparison -- July 27, 2018
Tagged as: [In an earlier post, I focused
on an in depth visit with CHAID (Chi-square automatic interaction
detection). Quoting myself, I said “As the name implies it is
fundamentally based on the venerable Chi-square test – and while not the
most powerful (in terms of detecting the smallest possible differences)
or the fastest, it really is easy to manage and more importantly to tell
the story after using it”. In this post I’ll spend a little time
comparing CHAID with a random forest algorithm in the ranger library
and with a gradient boosting algorithm via the xgboost library. I’ll
use the exact same data set for all three so we can draw some easy
comparisons about their speed and their accuracy.
I do believe CHAID is a great choice for some sets of data and some circumstances but I’m interested in some empirical information, so off we go.
Setup and library loading
If you’ve never used CHAID before you may also not have partykit.
CHAID isn’t on CRAN but I have provided the commented out install
command below. ranger and xgboost are available from CRAN and are
straightforward to install. You’ll also get a variety of messages, none
of which is relevant to this example so I’ve suppressed them.
# install.packages("partykit")
# install.packages("CHAID", repos="http://R-Forge.R-project.org")
# install.packages("ranger")
# install.packages("xgboost")
require(dplyr)
require(tidyr)
require(ggplot2)
require(CHAID)
require(purrr)
require(caret)
require(ranger)
require(xgboost)
require(kableExtra) # just to make the output nicer
theme_set(theme_bw()) # set theme for ggplot2
Predicting customer churn for a fictional TELCO company
We’re going to use a dataset that comes to us from the IBM Watson Project. It’s a very practical example and an understandable dataset. A great use case for the algorithms we’ll be using. Imagine yourself in a fictional company faced with the task of trying to predict which customers are going to leave your business for another provider a.k.a. churn. Obviously we’d like to be able to predict this phenomenon and potentially target these customers for retention or just better project our revenue. Being able to predict churn even a little bit better could save us lots of money, especially if we can identify the key indicators and influence them.
In the original posting I spent
a great deal of time explaining the mechanics of loading and prepping
the data. This time we’ll do that quickly and efficiently and if you
need an explanation of what’s going on please refer back. I’ve embedded
some comments in the code where I think they’ll be most helpful. First
we’ll grab the data from the IBM site using read.csv, in this case I’m
happy to let it tag most of our variables as factors since that’s what
we’ll want for our CHAID work.
set.seed(2018)
churn <- read.csv("https://community.watsonanalytics.com/wp-content/uploads/2015/03/WA_Fn-UseC_-Telco-Customer-Churn.csv")
str(churn)
## 'data.frame': 7043 obs. of 21 variables:
## $ customerID : Factor w/ 7043 levels "0002-ORFBO","0003-MKNFE",..: 5376 3963 2565 5536 6512 6552 1003 4771 5605 4535 ...
## $ gender : Factor w/ 2 levels "Female","Male": 1 2 2 2 1 1 2 1 1 2 ...
## $ SeniorCitizen : int 0 0 0 0 0 0 0 0 0 0 ...
## $ Partner : Factor w/ 2 levels "No","Yes": 2 1 1 1 1 1 1 1 2 1 ...
## $ Dependents : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 2 1 1 2 ...
## $ tenure : int 1 34 2 45 2 8 22 10 28 62 ...
## $ PhoneService : Factor w/ 2 levels "No","Yes": 1 2 2 1 2 2 2 1 2 2 ...
## $ MultipleLines : Factor w/ 3 levels "No","No phone service",..: 2 1 1 2 1 3 3 2 3 1 ...
## $ InternetService : Factor w/ 3 levels "DSL","Fiber optic",..: 1 1 1 1 2 2 2 1 2 1 ...
## $ OnlineSecurity : Factor w/ 3 levels "No","No internet service",..: 1 3 3 3 1 1 1 3 1 3 ...
## $ OnlineBackup : Factor w/ 3 levels "No","No internet service",..: 3 1 3 1 1 1 3 1 1 3 ...
## $ DeviceProtection: Factor w/ 3 levels "No","No internet service",..: 1 3 1 3 1 3 1 1 3 1 ...
## $ TechSupport : Factor w/ 3 levels "No","No internet service",..: 1 1 1 3 1 1 1 1 3 1 ...
## $ StreamingTV : Factor w/ 3 levels "No","No internet service",..: 1 1 1 1 1 3 3 1 3 1 ...
## $ StreamingMovies : Factor w/ 3 levels "No","No internet service",..: 1 1 1 1 1 3 1 1 3 1 ...
## $ Contract : Factor w/ 3 levels "Month-to-month",..: 1 2 1 2 1 1 1 1 1 2 ...
## $ PaperlessBilling: Factor w/ 2 levels "No","Yes": 2 1 2 1 2 2 2 1 2 1 ...
## $ PaymentMethod : Factor w/ 4 levels "Bank transfer (automatic)",..: 3 4 4 1 3 3 2 4 3 1 ...
## $ MonthlyCharges : num 29.9 57 53.9 42.3 70.7 ...
## $ TotalCharges : num 29.9 1889.5 108.2 1840.8 151.7 ...
## $ Churn : Factor w/ 2 levels "No","Yes": 1 1 2 1 2 2 1 1 2 1 ...
We have data on 7,043 customers across 21 variables. customerID can’t
really be a predictor but we will use it in a little bit. Churn is
what we want to predict so we have 19 potential predictor variables to
work with. Four of them were not automatically converted to factors so
we’ll have to look into them for CHAID. For a review of what the
output means and how CHAID works please refer
back.
Let’s address the easiest thing first. SeniorCitizen is coded zero and
one instead of yes/no so let’s recode that in a nice conservative
fashion and see what the breakdown is.
# Fix senior citizen status
churn$SeniorCitizen <- recode_factor(
churn$SeniorCitizen,
`0` = "No",
`1` = "Yes",
.default = "Should not happen"
)
summary(churn$SeniorCitizen)
## No Yes
## 5901 1142
We have three variables left that are numeric, now that we have
addressed senior citizen status. Let’s use a combination of dplyr and
ggplot2 to see what the distribution looks like using a density plot.
churn %>%
select_if(is.numeric) %>%
gather(metric, value) %>%
ggplot(aes(value, fill = metric)) +
geom_density(show.legend = FALSE) +
facet_wrap( ~ metric, scales = "free")
## Warning: Removed 11 rows containing non-finite values (stat_density).
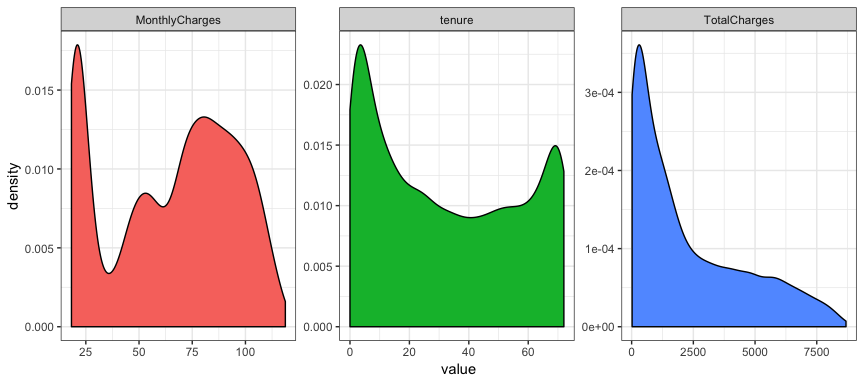
Well those aren’t the most normal looking distributions and we have this
message ## Warning: Removed 11 rows containing non-finite values
(stat_density). which alerts us to the fact that there are some missing
values in our data. Let’s first figure out where the missing data is:
churn %>%
select_if(anyNA) %>% summary
## TotalCharges
## Min. : 18.8
## 1st Qu.: 401.4
## Median :1397.5
## Mean :2283.3
## 3rd Qu.:3794.7
## Max. :8684.8
## NA's :11
Now we know that total customer charges is missing 11 entries. Our three algorithms vary as to how gracefully they handle missing values but at this point we have several options including:
- Eliminate the entire customer record if anything is missing
- Impute or substitute in some reasonable value like the mean or the median for missing values
- Do some fancier imputation to make sure we substitute in the most
plausible value for
TotalCharges
Elimination is easy, efficient, and conservative and since it is a very
small percentage of our total data set unlikely to cost us a lot of
information for the models that don’t handle missing values well. But
for purposes of this blog post and to help demonstrate some of the
capabilities within caret (since we’re going to use it anyway) we’ll
try median and knn (k nearest neighbor) imputation.
First let’s make a vector that contains the customerID numbers of the
eleven cases in question.
xxx <- churn %>%
filter_all(any_vars(is.na(.))) %>%
select(customerID)
xxx <- as.vector(xxx$customerID)
xxx
## [1] "4472-LVYGI" "3115-CZMZD" "5709-LVOEQ" "4367-NUYAO" "1371-DWPAZ" "7644-OMVMY" "3213-VVOLG" "2520-SGTTA" "2923-ARZLG" "4075-WKNIU" "2775-SEFEE"
churn %>% filter(customerID %in% xxx)
## customerID gender SeniorCitizen Partner Dependents tenure PhoneService MultipleLines InternetService OnlineSecurity OnlineBackup DeviceProtection TechSupport StreamingTV StreamingMovies Contract PaperlessBilling PaymentMethod MonthlyCharges TotalCharges Churn
## 1 4472-LVYGI Female No Yes Yes 0 No No phone service DSL Yes No Yes Yes Yes No Two year Yes Bank transfer (automatic) 52.55 NA No
## 2 3115-CZMZD Male No No Yes 0 Yes No No No internet service No internet service No internet service No internet service No internet service No internet service Two year No Mailed check 20.25 NA No
## 3 5709-LVOEQ Female No Yes Yes 0 Yes No DSL Yes Yes Yes No Yes Yes Two year No Mailed check 80.85 NA No
## 4 4367-NUYAO Male No Yes Yes 0 Yes Yes No No internet service No internet service No internet service No internet service No internet service No internet service Two year No Mailed check 25.75 NA No
## 5 1371-DWPAZ Female No Yes Yes 0 No No phone service DSL Yes Yes Yes Yes Yes No Two year No Credit card (automatic) 56.05 NA No
## 6 7644-OMVMY Male No Yes Yes 0 Yes No No No internet service No internet service No internet service No internet service No internet service No internet service Two year No Mailed check 19.85 NA No
## 7 3213-VVOLG Male No Yes Yes 0 Yes Yes No No internet service No internet service No internet service No internet service No internet service No internet service Two year No Mailed check 25.35 NA No
## 8 2520-SGTTA Female No Yes Yes 0 Yes No No No internet service No internet service No internet service No internet service No internet service No internet service Two year No Mailed check 20.00 NA No
## 9 2923-ARZLG Male No Yes Yes 0 Yes No No No internet service No internet service No internet service No internet service No internet service No internet service One year Yes Mailed check 19.70 NA No
## 10 4075-WKNIU Female No Yes Yes 0 Yes Yes DSL No Yes Yes Yes Yes No Two year No Mailed check 73.35 NA No
## 11 2775-SEFEE Male No No Yes 0 Yes Yes DSL Yes Yes No Yes No No Two year Yes Bank transfer (automatic) 61.90 NA No
As you look at those eleven records it doesn’t appear they are
“average”! In particular, I’m worried that the MonthlyCharges
look small and they have 0 tenure for this group. No way of knowing
for certain but it could be that these are just the newest customers
with very little time using our service. Let’s use our list to do some
comparing of these eleven versus the total population, that will help us
decide what to do about the missing cases. Replacing with the median
value is simple and easy but it may well not be the most accurate
choice.
churn %>%
filter(customerID %in% xxx) %>%
summarise(median(MonthlyCharges))
## median(MonthlyCharges)
## 1 25.75
median(churn$MonthlyCharges, na.rm = TRUE)
## [1] 70.35
churn %>%
filter(customerID %in% xxx) %>%
summarise(median(tenure))
## median(tenure)
## 1 0
median(churn$tenure, na.rm = TRUE)
## [1] 29
The median MonthlyCharges are much lower and instead of two years or
so of median tenure this group has none. Let’s use the preProcess
function in caret to accomplish several goals. We’ll ask it to impute
the missing values for us using both knnImpute (k nearest neighbors)
and a pure median medianImpute. From the ?preProcess help pages:
k-nearest neighbor imputation is carried out by finding the k closest samples (Euclidian distance) in the training set. Imputation via bagging fits a bagged tree model for each predictor (as a function of all the others). This method is simple, accurate and accepts missing values, but it has much higher computational cost. Imputation via medians takes the median of each predictor in the training set, and uses them to fill missing values. This method is simple, fast, and accepts missing values, but treats each predictor independently, and may be inaccurate.
We’ll also have it transform our numeric variables using YeoJohnson
and identify any predictor variables that have near zero variance nzv.
# using k nearest neighbors
pp_knn <- preProcess(churn, method = c("knnImpute", "YeoJohnson", "nzv"))
# simple output
pp_knn
## Created from 7032 samples and 21 variables
##
## Pre-processing:
## - centered (3)
## - ignored (18)
## - 5 nearest neighbor imputation (3)
## - scaled (3)
## - Yeo-Johnson transformation (3)
##
## Lambda estimates for Yeo-Johnson transformation:
## 0.45, 0.93, 0.25
# more verbose
pp_knn$method
## $knnImpute
## [1] "tenure" "MonthlyCharges" "TotalCharges"
##
## $YeoJohnson
## [1] "tenure" "MonthlyCharges" "TotalCharges"
##
## $ignore
## [1] "customerID" "gender" "SeniorCitizen" "Partner" "Dependents" "PhoneService" "MultipleLines" "InternetService" "OnlineSecurity" "OnlineBackup" "DeviceProtection" "TechSupport" "StreamingTV" "StreamingMovies" "Contract" "PaperlessBilling" "PaymentMethod" "Churn"
##
## $center
## [1] "tenure" "MonthlyCharges" "TotalCharges"
##
## $scale
## [1] "tenure" "MonthlyCharges" "TotalCharges"
# using medians
pp_median <- preProcess(churn, method = c("medianImpute", "YeoJohnson", "nzv"))
pp_median
## Created from 7032 samples and 21 variables
##
## Pre-processing:
## - ignored (18)
## - median imputation (3)
## - Yeo-Johnson transformation (3)
##
## Lambda estimates for Yeo-Johnson transformation:
## 0.45, 0.93, 0.25
pp_median$method
## $medianImpute
## [1] "tenure" "MonthlyCharges" "TotalCharges"
##
## $YeoJohnson
## [1] "tenure" "MonthlyCharges" "TotalCharges"
##
## $ignore
## [1] "customerID" "gender" "SeniorCitizen" "Partner" "Dependents" "PhoneService" "MultipleLines" "InternetService" "OnlineSecurity" "OnlineBackup" "DeviceProtection" "TechSupport" "StreamingTV" "StreamingMovies" "Contract" "PaperlessBilling" "PaymentMethod" "Churn"
The preProcess function creates a list object of class preProcess
that contains information about what needs to be done and what the
results of the transformations will be, but we need to apply the
predict function to actually make the changes proposed. So at this
point let’s create two new dataframes nchurn1 and nchurn2 that
contain the data after the pre-processing has occurred. Then we can see
how the results compare.
nchurn1 <- predict(pp_knn,churn)
nchurn2 <- predict(pp_median,churn)
nchurn2 %>%
filter(customerID %in% xxx) %>%
summarise(median(TotalCharges))
## median(TotalCharges)
## 1 20.79526
median(nchurn2$TotalCharges, na.rm = TRUE)
## [1] 20.79526
nchurn1 %>%
filter(customerID %in% xxx) %>%
summarise(median(TotalCharges))
## median(TotalCharges)
## 1 -1.849681
median(nchurn1$TotalCharges, na.rm = TRUE)
## [1] 0.01820494
May also be useful to visualize the data as we did earlier to see how the transformations have changed the density plots.
nchurn1 %>%
select_if(is.numeric) %>%
gather(metric, value) %>%
ggplot(aes(value, fill = metric)) +
geom_density(show.legend = FALSE) +
facet_wrap( ~ metric, scales = "free")
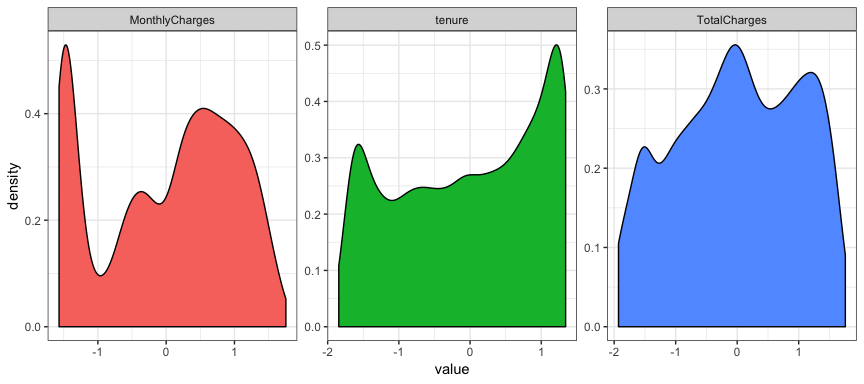
nchurn2 %>%
select_if(is.numeric) %>%
gather(metric, value) %>%
ggplot(aes(value, fill = metric)) +
geom_density(show.legend = FALSE) +
facet_wrap( ~ metric, scales = "free")
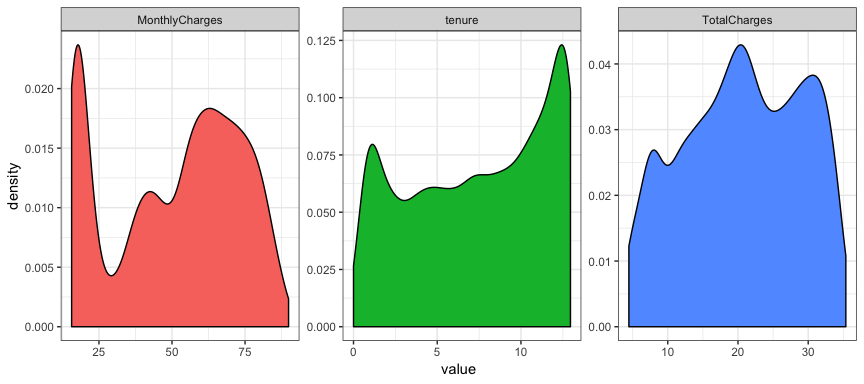
If you compare the two plots you can see that they vary imperceptibly
except for the y axis scale. There is no warning about missing values
and if you scroll back and compare with the original plots of the raw
variables the shape of tenure and TotalCharges have changed
significantly because of the transformation.
I’m pretty convinced that knn provides a much better approximation of those eleven missing values than a mere median substitution so let’s make those changes and move on to comparing models. While we’re at it, let’s go ahead and remove the unique customer ID number as well. We really only needed it to compare a few specific cases.
churn <- predict(pp_knn,churn)
churn$customerID <- NULL
str(churn)
## 'data.frame': 7043 obs. of 20 variables:
## $ gender : Factor w/ 2 levels "Female","Male": 1 2 2 2 1 1 2 1 1 2 ...
## $ SeniorCitizen : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ Partner : Factor w/ 2 levels "No","Yes": 2 1 1 1 1 1 1 1 2 1 ...
## $ Dependents : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 2 1 1 2 ...
## $ tenure : num -1.644 0.297 -1.495 0.646 -1.495 ...
## $ PhoneService : Factor w/ 2 levels "No","Yes": 1 2 2 1 2 2 2 1 2 2 ...
## $ MultipleLines : Factor w/ 3 levels "No","No phone service",..: 2 1 1 2 1 3 3 2 3 1 ...
## $ InternetService : Factor w/ 3 levels "DSL","Fiber optic",..: 1 1 1 1 2 2 2 1 2 1 ...
## $ OnlineSecurity : Factor w/ 3 levels "No","No internet service",..: 1 3 3 3 1 1 1 3 1 3 ...
## $ OnlineBackup : Factor w/ 3 levels "No","No internet service",..: 3 1 3 1 1 1 3 1 1 3 ...
## $ DeviceProtection: Factor w/ 3 levels "No","No internet service",..: 1 3 1 3 1 3 1 1 3 1 ...
## $ TechSupport : Factor w/ 3 levels "No","No internet service",..: 1 1 1 3 1 1 1 1 3 1 ...
## $ StreamingTV : Factor w/ 3 levels "No","No internet service",..: 1 1 1 1 1 3 3 1 3 1 ...
## $ StreamingMovies : Factor w/ 3 levels "No","No internet service",..: 1 1 1 1 1 3 1 1 3 1 ...
## $ Contract : Factor w/ 3 levels "Month-to-month",..: 1 2 1 2 1 1 1 1 1 2 ...
## $ PaperlessBilling: Factor w/ 2 levels "No","Yes": 2 1 2 1 2 2 2 1 2 1 ...
## $ PaymentMethod : Factor w/ 4 levels "Bank transfer (automatic)",..: 3 4 4 1 3 3 2 4 3 1 ...
## $ MonthlyCharges : num -1.158 -0.239 -0.343 -0.731 0.214 ...
## $ TotalCharges : num -1.81 0.254 -1.386 0.233 -1.249 ...
## $ Churn : Factor w/ 2 levels "No","Yes": 1 1 2 1 2 2 1 1 2 1 ...
One more step before we start using CHAID, ranger, and xgboost and
while we have the data in one frame. Let’s take the 3 numeric variables
and create 3 analogous variables as factors. This is necessary because
CHAID requires categorical a.k.a. nominal data. If you’d like to
review the options for how to “cut” the data please refer back to my
earlier post.
churn <- churn %>%
mutate_if(is.numeric,
funs(factor = cut_number(., n=5,
labels = c("Lowest","Below Middle","Middle","Above Middle","Highest"))))
summary(churn)
## gender SeniorCitizen Partner Dependents tenure PhoneService MultipleLines InternetService OnlineSecurity OnlineBackup DeviceProtection TechSupport StreamingTV StreamingMovies Contract PaperlessBilling PaymentMethod MonthlyCharges TotalCharges Churn tenure_factor MonthlyCharges_factor TotalCharges_factor
## Female:3488 No :5901 No :3641 No :4933 Min. :-1.8439 No : 682 No :3390 DSL :2421 No :3498 No :3088 No :3095 No :3473 No :2810 No :2785 Month-to-month:3875 No :2872 Bank transfer (automatic):1544 Min. :-1.5685 Min. :-1.929306 No :5174 Lowest :1481 Lowest :1420 Lowest :1409
## Male :3555 Yes:1142 Yes:3402 Yes:2110 1st Qu.:-0.8555 Yes:6361 No phone service: 682 Fiber optic:3096 No internet service:1526 No internet service:1526 No internet service:1526 No internet service:1526 No internet service:1526 No internet service:1526 One year :1473 Yes:4171 Credit card (automatic) :1522 1st Qu.:-0.9632 1st Qu.:-0.783551 Yes:1869 Below Middle:1397 Below Middle:1397 Below Middle:1408
## Median : 0.1183 Yes :2971 No :1526 Yes :2019 Yes :2429 Yes :2422 Yes :2044 Yes :2707 Yes :2732 Two year :1695 Electronic check :2365 Median : 0.2021 Median : 0.018205 Middle :1408 Middle :1411 Middle :1409
## Mean : 0.0000 Mailed check :1612 Mean : 0.0000 Mean :-0.002732 Above Middle:1350 Above Middle:1407 Above Middle:1408
## 3rd Qu.: 0.9252 3rd Qu.: 0.8341 3rd Qu.: 0.868066 Highest :1407 Highest :1408 Highest :1409
## Max. : 1.3421 Max. : 1.7530 Max. : 1.758003
Okay now we have three additional variables that end in _factor, they’re like their numeric equivalents only cut into more or less 5 equal bins.
Training and testing our models
We’re going to use caret to train and test all three of the algorithms
on our data. We could operate directly by invoking the individual model
functions directly but caret will allow us to use some common steps.
We’ll employ cross-validation a.k.a. cv to mitigate the problem of
over-fitting. This article
explains
it well so I won’t repeat that explanation here, I’ll simply show you
how to run the steps in R.
This is also a good time to point out that caret has extraordinarily
comprehensive documentation which I
used extensively and I’m limiting myself to the basics.
As a first step, let’s just take 30% of our data and put is aside as the
testing data set. Why 30%? Doesn’t have to be, could be as low as 20% or
as high as 40% it really depends on how conservative you want to be, and
how much data you have at hand. Since this is just a tutorial we’ll
simply use 30% as a representative number. I’m going to use caret
syntax which is the line with createDataPartition(churn$Churn, p=0.7,
list=FALSE) in it. That takes our data set churn makes a 70% split
ensuring that we keep our outcome variable Churn as close to 70/30 as
we can. This is important because our data is already pretty lop-sided
for outcomes. The two subsequent lines serve to take the vector
intrain and produce two separate dataframes, testing and training.
They have 2112 and 4931 customers respectively.
intrain <- createDataPartition(churn$Churn, p=0.7, list=FALSE)
training <- churn[intrain,]
testing <- churn[-intrain,]
dim(training)
## [1] 4931 23
dim(testing)
## [1] 2112 23
CHAID
Now that we have a training and testing dataset let’s remove the numeric
version of the variables CHAID can’t use.
# first pass at CHAID
# remove numbers
training <- training %>%
select_if(is.factor)
dim(training)
## [1] 4931 20
testing <- testing %>%
select_if(is.factor)
dim(testing)
## [1] 2112 20
The next step is a little counter-intuitive but quite practical. Turns
out that many models do not perform well when you feed them a formula
for the model even if they claim to support a formula interface (as
CHAID does). Here’s a Stack Overflow
link
that discusses in detail but my suggestion to you is to always separate
them and avoid the problem altogether. We’re just taking our
predictors or features and putting them in x while we put our
outcome in y.
# create response and feature data
features <- setdiff(names(training), "Churn")
x <- training[, features]
y <- training$Churn
trainControl is the next function within caret we need to use.
Chapter 5 in the caret doco covers it in great detail. I’m simply
going to pluck out a few sane and safe options. method = "cv" gets us
cross-validation. number = 5 is pretty obvious. I happen to like
seeing the progress in case I want to go for coffee so verboseIter =
TRUE (here I will turn it off since the static output is rather
boring), and I play it safe and explicitly save my predictions
savePredictions = "final". We put everything in train_control which
we’ll use in a minute. We’ll use this same train_control for all our
models
# set up 5-fold cross validation procedure
train_control <- trainControl(method = "cv",
number = 5,
# verboseIter = TRUE,
savePredictions = "final")
By default caret allows us to adjust three parameters in our chaid
model; alpha2, alpha3, and alpha4. As a matter of fact it will
allow us to build a grid of those parameters and test all the
permutations we like, using the same cross-validation process. I’m a bit
worried that we’re not being conservative enough. I’d like to train our
model using p values for alpha that are not .05, .03, and .01 but
instead the de facto levels in my discipline; .05, .01, and .001. The
function in caret is tuneGrid. We’ll use the base R function
expand.grid to build a dataframe with all the combinations and then
feed it to caret in our training via tuneGrid = search_grid in our
call to train.
# set up tuning grid default
search_grid <- expand.grid(
alpha2 = c(.05, .01, .001),
alpha4 = c(.05, .01, .001),
alpha3 = -1
)
Now we can use the train function in caret to train our model! It
wants to know what our x and y’s are, as well as our training
control parameters which we’ve parked in train_control.
chaid.model <- train(
x = x,
y = y,
method = "chaid",
trControl = train_control,
tuneGrid = search_grid
)
chaid.model
## CHi-squared Automated Interaction Detection
##
## 4931 samples
## 19 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 3944, 3946, 3945, 3944, 3945
## Resampling results across tuning parameters:
##
## alpha2 alpha4 Accuracy Kappa
## 0.001 0.001 0.7805723 0.3956853
## 0.001 0.010 0.7832088 0.3786619
## 0.001 0.050 0.7767165 0.3956067
## 0.010 0.001 0.7844263 0.3950757
## 0.010 0.010 0.7832088 0.3740510
## 0.010 0.050 0.7767167 0.3883397
## 0.050 0.001 0.7844263 0.3950757
## 0.050 0.010 0.7817889 0.3764934
## 0.050 0.050 0.7783394 0.3921129
##
## Tuning parameter 'alpha3' was held constant at a value of -1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were alpha2 = 0.05, alpha3 = -1 and alpha4 = 0.001.
And after roughly two minutes it’s done. Let’s inspect what we have so
far. The output gives us a nice concise summary. 4931 cases with 19
predictors. It gives us an idea of how many of the 4931 cases were used
in the individual folds Summary of sample
sizes: 3944, 3946, 3945, 3944, 3945. If you need a review of what
alpha2, alpha4, and alpha3 are please review the ?chaid doco.
You’ll notice that I stored the results in an object called
chaid.model. That object has lots of useful information you can access
(it’s a list object of class “train”). As a matter of fact we will be
creating one object per run and then using the stored information to
build a nice comparison later. For now here are some useful examples of
what’s contained in the object…
- Produce the
confusionMatrixacross all foldsconfusionMatrix(chaid.model) - Plot the effect of the tuning parameters on accuracy
plot(chaid.model). Note that the scaling deceives the eye and the results are close across the plot - Check on variable importance
varImp(chaid.model) - How long did it take? Look in
chaid.model$times
If you need a refresher on what these represent please see the earlier post on CHAID.
confusionMatrix(chaid.model)
## Cross-Validated (5 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 66.2 14.3
## Yes 7.2 12.2
##
## Accuracy (average) : 0.7844
plot(chaid.model)
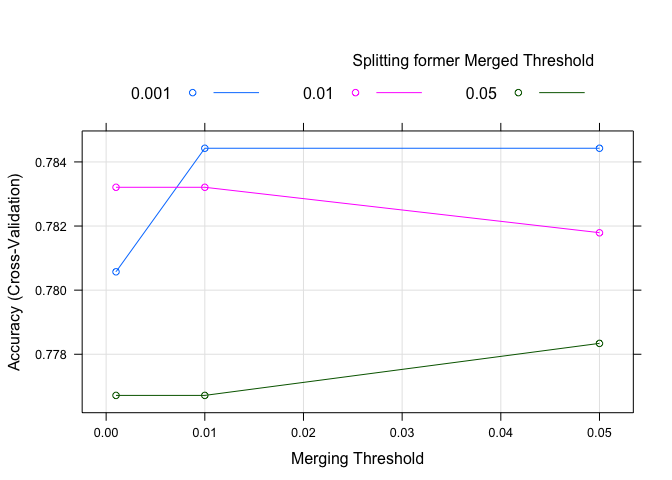
varImp(chaid.model)
## ROC curve variable importance
##
## Importance
## Contract 100.0000
## tenure_factor 95.7457
## OnlineSecurity 81.2110
## TechSupport 74.1473
## TotalCharges_factor 57.0885
## MonthlyCharges_factor 53.3755
## OnlineBackup 48.3382
## DeviceProtection 45.3815
## PaperlessBilling 44.2540
## Partner 36.7387
## Dependents 35.4481
## PaymentMethod 29.7699
## SeniorCitizen 22.5287
## StreamingMovies 10.3811
## MultipleLines 9.1536
## InternetService 7.8258
## StreamingTV 6.7502
## gender 0.6105
## PhoneService 0.0000
chaid.model$times
## $everything
## user system elapsed
## 131.788 1.824 133.819
##
## $final
## user system elapsed
## 1.393 0.028 1.425
##
## $prediction
## [1] NA NA NA
One of the nice aspects about CHAID as a method is that is relatively
easy to “see”” your model in either text or plot format. While there are
packages that will help you “see” a random forest; by definition (pardon
the pun) it’s hard to see the forest because of all the trees. Simply
“printing” the final model with chaid.model$finalModel gives you the
text representation while you can plot the final model with
plot(chaid.model$finalModel). As I explained in the earlier post it’s
nice being able to see where your model fits well and where it misses at
a high level.
chaid.model$finalModel
##
## Model formula:
## .outcome ~ gender + SeniorCitizen + Partner + Dependents + PhoneService +
## MultipleLines + InternetService + OnlineSecurity + OnlineBackup +
## DeviceProtection + TechSupport + StreamingTV + StreamingMovies +
## Contract + PaperlessBilling + PaymentMethod + tenure_factor +
## MonthlyCharges_factor + TotalCharges_factor
##
## Fitted party:
## [1] root
## | [2] Contract in Month-to-month
## | | [3] InternetService in DSL
## | | | [4] TotalCharges_factor in Lowest: No (n = 326, err = 49.7%)
## | | | [5] TotalCharges_factor in Below Middle: No (n = 255, err = 27.5%)
## | | | [6] TotalCharges_factor in Middle, Above Middle, Highest: No (n = 282, err = 15.2%)
## | | [7] InternetService in Fiber optic
## | | | [8] tenure_factor in Lowest
## | | | | [9] OnlineSecurity in No, No internet service: Yes (n = 414, err = 25.4%)
## | | | | [10] OnlineSecurity in Yes: No (n = 33, err = 42.4%)
## | | | [11] tenure_factor in Below Middle: Yes (n = 413, err = 41.4%)
## | | | [12] tenure_factor in Middle: No (n = 352, err = 44.3%)
## | | | [13] tenure_factor in Above Middle, Highest: No (n = 276, err = 31.9%)
## | | [14] InternetService in No: No (n = 378, err = 17.2%)
## | [15] Contract in One year
## | | [16] StreamingMovies in No: No (n = 303, err = 8.3%)
## | | [17] StreamingMovies in No internet service: No (n = 268, err = 2.2%)
## | | [18] StreamingMovies in Yes: No (n = 457, err = 20.6%)
## | [19] Contract in Two year
## | | [20] InternetService in DSL, No: No (n = 866, err = 1.2%)
## | | [21] InternetService in Fiber optic: No (n = 308, err = 8.1%)
##
## Number of inner nodes: 7
## Number of terminal nodes: 14
plot(chaid.model$finalModel)
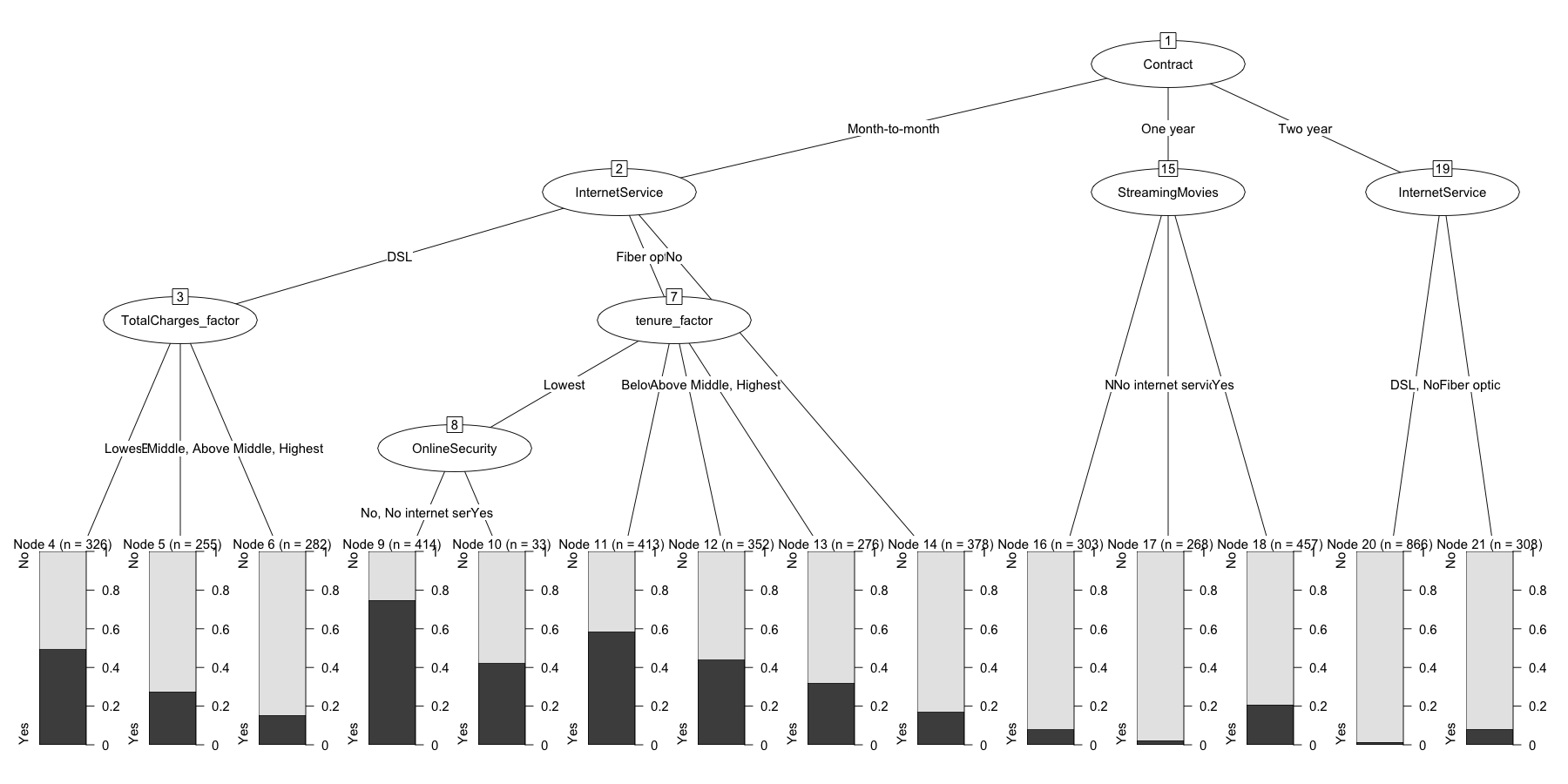
Finally, probably the most important step of all, we’ll take our trained
model and apply it to the testing data that we held back to see how
well it fits this data it’s never seen before. This is a key step
because it reassures us that we have not overfit (if you want a fuller
understanding please consider reading this post on EliteDataScience) our
model.
We’ll take our model we made with the training dataset chaid.model
and have it predict against the testing dataset and see how we did with
a confusionMatrix
confusionMatrix(predict(chaid.model, newdata = testing), testing$Churn)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 1443 331
## Yes 109 229
##
## Accuracy : 0.7917
## 95% CI : (0.7737, 0.8088)
## No Information Rate : 0.7348
## P-Value [Acc > NIR] : 7.793e-10
##
## Kappa : 0.3878
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9298
## Specificity : 0.4089
## Pos Pred Value : 0.8134
## Neg Pred Value : 0.6775
## Prevalence : 0.7348
## Detection Rate : 0.6832
## Detection Prevalence : 0.8400
## Balanced Accuracy : 0.6693
##
## 'Positive' Class : No
##
Very nice! Our accuracy on testing actually exceeds the accuracy we
achieved in training.
Random Forest via ranger
One of the nicest things about using caret is that it is pretty
straight-forward to move from one model to another. The amount of work
we have to do while moving from CHAID to ranger and eventually
xgboost is actually quite modest.
ranger will accept a mix of factors and numeric variables so our first
step will be to go back and recreate training and testing using the
numeric versions of tenure, MonthlyCharges, and TotalCharges
instead of the _factor versions. intrain still holds our list of rows
that should be in training so we’ll follow the exact same process just
keep the numeric versions and arrive at x and y to feed to caret
and ranger.
##### using ranger
# intrain <- createDataPartition(churn$Churn,p=0.7,list=FALSE)
training <- churn[intrain,]
testing <- churn[-intrain,]
dim(training)
## [1] 4931 23
dim(testing)
## [1] 2112 23
training <- training %>%
select(-ends_with("_factor"))
dim(training)
## [1] 4931 20
# testing <- testing %>%
# select(-ends_with("_factor"))
dim(testing)
## [1] 2112 23
# create response and feature data
features <- setdiff(names(training), "Churn")
x <- training[, features]
y <- training$Churn
As I mentioned earlier train_control doesn’t have to change at all. So
I’ll just print it to remind you of what’s in there.
search_grid is almost always specific to the model and this is no
exception. When we consult the documentation for ranger within
caret
we see that we can adjust mtry, splitrule, and min.node.size.
We’ll put in some reasonable values for those and then put the
resulting grid into rf_grid. I tried to give ranger’s search grid about
the same amount of flexibility as I did for CHAID.
##### reusing train_control
head(train_control)
## $method
## [1] "cv"
##
## $number
## [1] 5
##
## $repeats
## [1] NA
##
## $search
## [1] "grid"
##
## $p
## [1] 0.75
##
## $initialWindow
## NULL
# define a grid of parameter options to try with ranger
rf_grid <- expand.grid(mtry = c(2:4),
splitrule = c("gini"),
min.node.size = c(3, 5, 7))
rf_grid
## mtry splitrule min.node.size
## 1 2 gini 3
## 2 3 gini 3
## 3 4 gini 3
## 4 2 gini 5
## 5 3 gini 5
## 6 4 gini 5
## 7 2 gini 7
## 8 3 gini 7
## 9 4 gini 7
Okay, we’re ready to train our model using ranger now. The only
additional line we need (besides changing from chaid to ranger is to
tell it what to use to capture variable importance e.g. “impurity”.
# re-fit the model with the parameter grid
rf.model <- train(
x = x,
y = y,
method = "ranger",
trControl = train_control,
tuneGrid = rf_grid,
importance = "impurity")
rf.model
## Random Forest
##
## 4931 samples
## 19 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 3946, 3944, 3945, 3944, 3945
## Resampling results across tuning parameters:
##
## mtry min.node.size Accuracy Kappa
## 2 3 0.7990299 0.4368130
## 2 5 0.8000437 0.4380797
## 2 7 0.7976106 0.4298171
## 3 3 0.7963928 0.4342273
## 3 5 0.7980151 0.4365761
## 3 7 0.7986242 0.4360132
## 4 3 0.7970009 0.4343468
## 4 5 0.7982171 0.4358659
## 4 7 0.7943648 0.4228518
##
## Tuning parameter 'splitrule' was held constant at a value of gini
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were mtry = 2, splitrule = gini and min.node.size = 5.
Now we can run the exact same set of commands as we did with chaid.model on rf.model.
confusionMatrix(rf.model)
## Cross-Validated (5 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 67.1 13.6
## Yes 6.4 12.9
##
## Accuracy (average) : 0.8
plot(rf.model)
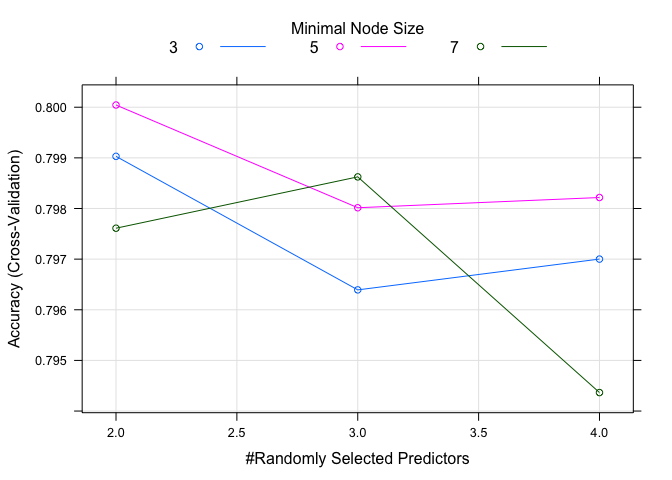
varImp(rf.model)
## ranger variable importance
##
## Overall
## tenure 100.000
## TotalCharges 97.336
## MonthlyCharges 88.321
## Contract 66.882
## OnlineSecurity 43.533
## TechSupport 37.978
## PaymentMethod 34.685
## InternetService 29.435
## OnlineBackup 18.389
## DeviceProtection 14.376
## PaperlessBilling 13.363
## MultipleLines 10.114
## Partner 9.712
## StreamingTV 9.607
## StreamingMovies 8.183
## gender 7.998
## Dependents 7.679
## SeniorCitizen 7.314
## PhoneService 0.000
rf.model$times
## $everything
## user system elapsed
## 110.338 1.543 18.646
##
## $final
## user system elapsed
## 2.205 0.023 0.346
##
## $prediction
## [1] NA NA NA
Now, the all important prediction against the testing data set.
confusionMatrix(predict(rf.model, newdata = testing), testing$Churn)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 1427 286
## Yes 125 274
##
## Accuracy : 0.8054
## 95% CI : (0.7879, 0.8221)
## No Information Rate : 0.7348
## P-Value [Acc > NIR] : 2.048e-14
##
## Kappa : 0.4501
## Mcnemar's Test P-Value : 2.969e-15
##
## Sensitivity : 0.9195
## Specificity : 0.4893
## Pos Pred Value : 0.8330
## Neg Pred Value : 0.6867
## Prevalence : 0.7348
## Detection Rate : 0.6757
## Detection Prevalence : 0.8111
## Balanced Accuracy : 0.7044
##
## 'Positive' Class : No
##
Very nice! Once again our accuracy on testing actually exceeds the accuracy we achieved in training. Looks like we were more accurate than CHAID but we’ll come back to that after we finish xgboost.
Extreme Gradient Boosting via xgboost
Moving from ranger to xgboost is even easier than it was from
CHAID.
xgboost like ranger will accept a mix of factors and numeric
variables so there is no need to change our training and testing
datasets at all. There’s also no need to change our train_control. As
far as tuning goes caret supports 7 of the many
parameters that
you could feed to ?xgboost. If you consult the caret documentation
here under
xgbTree you’ll see them listed. If you don’t provide any tuning
guidance then it will provide a default set of pretty rational initial
values. I initially ran it that way but below for purposes of this post
have chosen only a few that seem to make the largest difference to
accuracy and set the rest to a constant.
One final important note about the code below. Notice in the train
command I am feeding a formula Churn ~ . to train. If you try to
give it the same x = x & y = y syntax I used with ranger it will fail.
That’s because as stated in the doco “xgb.train accepts only an
xgb.DMatrix as the input. xgboost, in addition, also accepts matrix,
dgCMatrix, or name of a local data file.” You could use commands like
xx <- model.matrix(~. -1, data=x)[,-1] & yy <- as.numeric(y) -1 to
convert them but since our dataset is small I’m just going to use the
formula interface.
# reusing train_control
head(train_control)
## $method
## [1] "cv"
##
## $number
## [1] 5
##
## $repeats
## [1] NA
##
## $search
## [1] "grid"
##
## $p
## [1] 0.75
##
## $initialWindow
## NULL
# define a grid of parameter options to try with xgboost
xgb_grid <- expand.grid(nrounds = c(100, 150, 200),
max_depth = 1,
min_child_weight = 1,
subsample = 1,
gamma = 0,
colsample_bytree = 0.8,
eta = c(.2, .3, .4))
xgb_grid
## nrounds max_depth min_child_weight subsample gamma colsample_bytree eta
## 1 100 1 1 1 0 0.8 0.2
## 2 150 1 1 1 0 0.8 0.2
## 3 200 1 1 1 0 0.8 0.2
## 4 100 1 1 1 0 0.8 0.3
## 5 150 1 1 1 0 0.8 0.3
## 6 200 1 1 1 0 0.8 0.3
## 7 100 1 1 1 0 0.8 0.4
## 8 150 1 1 1 0 0.8 0.4
## 9 200 1 1 1 0 0.8 0.4
# Fit the model with the parameter grid
xgboost.model <- train(Churn ~ .,
training ,
method = "xgbTree",
tuneGrid = xgb_grid,
trControl = train_control)
xgboost.model
## eXtreme Gradient Boosting
##
## 4931 samples
## 19 predictor
## 2 classes: 'No', 'Yes'
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 3945, 3944, 3945, 3944, 3946
## Resampling results across tuning parameters:
##
## eta nrounds Accuracy Kappa
## 0.2 100 0.7974010 0.4272991
## 0.2 150 0.7998353 0.4414212
## 0.2 200 0.8002400 0.4465105
## 0.3 100 0.8002410 0.4449462
## 0.3 150 0.8020667 0.4532478
## 0.3 200 0.8028779 0.4565789
## 0.4 100 0.8010528 0.4478758
## 0.4 150 0.8020655 0.4530151
## 0.4 200 0.8024716 0.4546512
##
## Tuning parameter 'max_depth' was held constant at a value of 1
## Tuning parameter 'gamma' was held constant at a value of 0
## Tuning parameter 'colsample_bytree' was held constant at a value of 0.8
## Tuning parameter 'min_child_weight' was held constant at a value of 1
## Tuning parameter 'subsample' was held constant at a value of 1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were nrounds = 200, max_depth = 1, eta = 0.3, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1 and subsample = 1.
After a (relatively) brief moment the results are back. Average accuracy
on the training is .8029 which is better than CHAID or ranger. We
can run the same additional commands simply by listing xgboost.model.
confusionMatrix(xgboost.model)
## Cross-Validated (5 fold) Confusion Matrix
##
## (entries are percentual average cell counts across resamples)
##
## Reference
## Prediction No Yes
## No 66.5 12.7
## Yes 7.0 13.8
##
## Accuracy (average) : 0.8029
plot(xgboost.model)
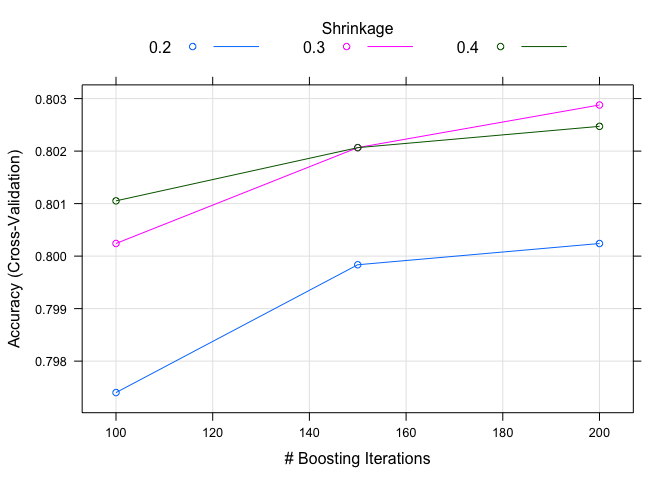
varImp(xgboost.model)
## xgbTree variable importance
##
## only 20 most important variables shown (out of 30)
##
## Overall
## tenure 100.00000
## InternetServiceFiber optic 64.17202
## ContractTwo year 48.23551
## InternetServiceNo 26.81070
## ContractOne year 10.38092
## OnlineSecurityYes 7.23882
## StreamingTVYes 5.04154
## MultipleLinesYes 2.87755
## StreamingMoviesYes 2.74796
## TechSupportYes 2.14009
## PhoneServiceYes 1.52273
## DependentsYes 1.33244
## SeniorCitizenYes 0.50710
## genderMale 0.23151
## DeviceProtectionYes 0.03949
## MonthlyCharges 0.00000
## MultipleLinesNo phone service 0.00000
## StreamingMoviesNo internet service 0.00000
## OnlineBackupNo internet service 0.00000
## PartnerYes 0.00000
xgboost.model$times
## $everything
## user system elapsed
## 4.635 0.038 4.681
##
## $final
## user system elapsed
## 0.263 0.002 0.266
##
## $prediction
## [1] NA NA NA
Now, the all important prediction against the testing data set.
confusionMatrix(predict(xgboost.model, newdata = testing), testing$Churn)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 1405 262
## Yes 147 298
##
## Accuracy : 0.8063
## 95% CI : (0.7888, 0.823)
## No Information Rate : 0.7348
## P-Value [Acc > NIR] : 9.038e-15
##
## Kappa : 0.4682
## Mcnemar's Test P-Value : 1.731e-08
##
## Sensitivity : 0.9053
## Specificity : 0.5321
## Pos Pred Value : 0.8428
## Neg Pred Value : 0.6697
## Prevalence : 0.7348
## Detection Rate : 0.6652
## Detection Prevalence : 0.7893
## Balanced Accuracy : 0.7187
##
## 'Positive' Class : No
##
Very nice! Once again our accuracy on testing .8063 actually exceeds the accuracy we achieved in training. Looks like we were more accurate than either CHAID or ranger and we’ll focus on the comparison in the next section.
Comparing Models
At this juncture we’re faced with a problem I’ve had before. We’re
drowning in data from the individual confusionMatrix results. We’ll
resort to the same purrr
solution to give us a far
more legible table of results focusing on the metrics I’m most
interested in. To do that we need to:
- Make a
named listcalledmodellistthat contains our 3 models with a descriptive name for each - Use
mapfrompurrrto apply thepredictcommand to each model in turn to ourtestingdataset - Pipe those results to a second
mapcommand to generate a confusion matrix comparing our predictions totesting$Churnwhich are the actual outcomes. - Pipe those results to a complex
map_dfr(that I explained previously) that creates a dataframe of all the results with each model as a row. - Separately grab the elapsed times for training with commands like
chaid.model$times$everything[[3]] - Separately grab the best accuracy for training with commands like
max(chaid.model$results$Accuracy) - Then use
kableto make a pretty table that is much easier to understand.
modellist <- list("CHAID" = chaid.model,
"ranger" = rf.model,
"xgboost" = xgboost.model)
CompareResults <- map(modellist, ~ predict(.x, newdata = testing)) %>%
map(~ confusionMatrix(testing$Churn, .x)) %>%
map_dfr(~ cbind(as.data.frame(t(.x$overall)),
as.data.frame(t(.x$byClass))),
.id = "Model")
CompareResults[1,"ETime"] <- chaid.model$times$everything[[3]]
CompareResults[2,"ETime"] <- rf.model$times$everything[[3]]
CompareResults[3,"ETime"] <- xgboost.model$times$everything[[3]]
CompareResults[1,"BestTrain"] <- max(chaid.model$results$Accuracy)
CompareResults[2,"BestTrain"] <- max(rf.model$results$Accuracy)
CompareResults[3,"BestTrain"] <- max(xgboost.model$results$Accuracy)
kable(CompareResults, "html") %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))
| Model | Accuracy | Kappa | AccuracyLower | AccuracyUpper | AccuracyNull | AccuracyPValue | McnemarPValue | Sensitivity | Specificity | Pos Pred Value | Neg Pred Value | Precision | Recall | F1 | Prevalence | Detection Rate | Detection Prevalence | Balanced Accuracy | ETime | BestTrain |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CHAID | 0.7916667 | 0.3878325 | 0.7737107 | 0.8088094 | 0.8399621 | 1.0000000 | 0 | 0.8134160 | 0.6775148 | 0.9297680 | 0.4089286 | 0.9297680 | 0.8134160 | 0.8677090 | 0.8399621 | 0.6832386 | 0.7348485 | 0.7454654 | 133.819 | 0.7844263 |
| ranger | 0.8053977 | 0.4501003 | 0.7878577 | 0.8220858 | 0.8110795 | 0.7573566 | 0 | 0.8330414 | 0.6867168 | 0.9194588 | 0.4892857 | 0.9194588 | 0.8330414 | 0.8741194 | 0.8110795 | 0.6756629 | 0.7348485 | 0.7598791 | 18.646 | 0.8000437 |
| xgboost | 0.8063447 | 0.4681509 | 0.7888346 | 0.8230002 | 0.7892992 | 0.0281863 | 0 | 0.8428314 | 0.6696629 | 0.9052835 | 0.5321429 | 0.9052835 | 0.8428314 | 0.8729419 | 0.7892992 | 0.6652462 | 0.7348485 | 0.7562472 | 4.681 | 0.8028779 |
What do we know?
Well our table looks very nice but there’s probably still too much information. What data should we focus on and what conclusions can we draw from our little exercise in comparative modeling? I will draw your attention back to this webpage to review the terminology for classification models and how to interpret a confusion matrix.
So Accuracy, Kappa, and F1 are all measures of overall accuracy.
There are merits to each. Pos Pred Value, and Neg Pred Value are
related but different nuanced ideas we’ll discuss in a minute. We’ll
also want to talk about time to complete training our model with ETime
and training accuracy with BestTrain.
Let’s use dplyr to select just these columns we want and see what we
can glean from this reduced table.
CompareResults %>%
select(Model, ETime, BestTrain, Accuracy, Kappa, F1, 'Pos Pred Value', 'Neg Pred Value') %>%
kable("html") %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))
| Model | ETime | BestTrain | Accuracy | Kappa | F1 | Pos Pred Value | Neg Pred Value |
|---|---|---|---|---|---|---|---|
| CHAID | 133.819 | 0.7844263 | 0.7916667 | 0.3878325 | 0.8677090 | 0.9297680 | 0.4089286 |
| ranger | 18.646 | 0.8000437 | 0.8053977 | 0.4501003 | 0.8741194 | 0.9194588 | 0.4892857 |
| xgboost | 4.681 | 0.8028779 | 0.8063447 | 0.4681509 | 0.8729419 | 0.9052835 | 0.5321429 |
Clearly xgboost is the fastest to train a model, more than 30 times
faster than CHAID, and 3 times faster than ranger for this data. Not
really surprising since xgboost is a very modern set of code designed
from the ground up to be fast and
efficient.
One interesting fact you can glean from all 3 models is that they all
did better on testing than they did on training. This is slightly
unusual since one would expect some differences to be missed but is
likely simply due to a lucky split in our data with more of the
difficult to predict cases falling in training than testing. The
good news is it leaves us feeling comfortable that we did not overfit
our model to the training data, which is why we were conservative in our
fitting and cross validated the training data.
No matter which “accuracy measure” we look at Accuracy, F1 or
Kappa the answer is pretty consistent, xgboost “wins” or is the most
accurate. The exception is F1 where ranger edges is out by 0.11775%
which means it was correct on about 3 more cases out of 2112 cases in
the testing set.
Notice that the differences in accuracy are not large as percentages
xgboost is 1.4678% more accurate than CHAID or it correctly
predicted 31 more customers. While more accurate is always “better” the
practical significance is also a matter of what the stakes are. If a
wrong prediction costs you $1,000.00 dollars that additional accuracy is
more concerning than a lesser dollar amount.
I also deliberately included Positive and Negative Predictive
Values
the columns labelled Pos Pred Value and Neg Pred Value for a very
specific reason. Notice that CHAID has the highest Pos Pred Value
that means is is the most accurate at predicting customers who did not
“churn”. Of the 1,552 customers who did not leave us is correctly
predicted 1,443 of them. xgboost on the other hand was much much
better at Neg Pred Value correctly predicting 298 out of 560 customers
who left us. While Accuracy, Kappa and F1 take different
approaches to finding “balanced” accuracy sometimes one case negative or
positive has more important implications for your business and you
should choose those measures.
At least at this point after a possible tl;dr journey we have some empirical data to inform my original statement about CHAID: “As the name implies it is fundamentally based on the venerable Chi-square test – and while not the most powerful (in terms of detecting the smallest possible differences) or the fastest, it really is easy to manage and more importantly to tell the story after using it”.
What don’t we know?
-
That this example would apply to other types of datasets. Absolutely not! This sort of data is almost ideal for CHAID since it involves a lot of nominal/categorical and/or ordinal data. CHAID will get much slower faster as we add more columns. More generally this was one example relatively small dataset more about learning something about
caretand process than a true comparison of accuracy across a wide range of cases. -
This is the “best” these models can do with this data Absolutely not! I made no attempt to seriously tune any of them. Tried some mild comparability. Also made no effort to feature engineer or adjust. I’m pretty certain if you tried you can squeeze a little more out of all three. Even wth
CHAIDthere’s more we could do very easily. I arbitrarily dividedtenureinto 5 equal sized bins. Why not 10? Why not equidistant instead of equal sized?
Done!
I hope you’ve found this useful. I am always open to comments, corrections and suggestions.
Chuck (ibecav at gmail dot com)
License

This
work is licensed under a
Creative
Commons Attribution-ShareAlike 4.0 International License.